หลังจากที่เขียน tutorial ใน Medium เลยอยากลองเปลี่ยนบรรยากาศมาเขียนเว็บตัวเอง (แบบง่อย ๆ) ดูบ้าง เนื่องจากว่าใกล้ ๆ นี้จะมีการแข่ง TOI15 พอดี เพราะฉะนั้นขอเปิดด้วยการเขียน tutorial เรื่อง Binary Search เลยละกัน!

Table of Contents

• รู้จักกับ Binary Search
• วิธีการเขียนโค้ด Binary Search
  • Iterative Binary Search
  • Recursive Binary Search
  • ปัญหาที่พบบ่อยในการเขียนโค้ด Binary Search
• ตัวอย่างการดัดแปลง Binary Search
  • หาจำนวนแรกที่มีค่ามากกว่า $x$
  • หาจุดวิกฤตใน Bitonic Sequence
• การใช้ Binary Search ในการแก้ Optimization Problem
  • คำอธิบายโจทย์
  • ข้อสังเกตเกี่ยวกับโจทย์
  • Implementation
  • Time Complexity
• บทสรุป

สมมุติว่ามี array $A$ ซึ่งประกอบไปด้วยจำนวนเต็มทั้งหมด $n$ ตัว จงเขียนโปรแกรมเพื่อตอบว่ามีจำนวนเต็ม $x$ อยู่ใน $A$ หรือไม่ (อาจจะถามคำถามหลายครั้ง)

วิธีหนึ่งที่ง่ายที่สุดก็คงไม่พ้นการลูปดูแต่ละช่องของ $A$ จนกว่าจะเจอเลขที่เราต้องการ วิธีนี้เรียกว่า Linear Search

bool linear_search(int n, int A[], int x) {
    for (int i = 0; i < n; ++i) {
        if (A[i] == x)
            return true;
    }
    return false;
}

ถึงอย่างไรก็ตาม ในกรณีแย่สุด วิธีนี้อาจจะใช้เวลาทำงาน $\mathcal{O}(n)$ ต่อการค้นหาหนึ่งครั้ง เพราะตัวเลขที่เราต้องการอาจจะอยู่ท้าย ๆ ของ array หรืออาจจะไม่มีอยู่ใน array เลยก็ได้

เพื่อให้โปรแกรมมีประสิทธิภาพมากขึ้น เราจำเป็นต้องหาวิธีที่สามารถตอบคำถามดังกล่าวได้รวดเร็วกว่าเดิม

รู้จักกับ Binary Search

ถ้าสมาชิกใน $A$ มีค่าเรียงจากน้อยไปมาก เราจะสามารถหาค่า $x$ ได้รวดเร็วมากขึ้น โดยใช้วิธี Binary Search ดังนี้

• ลองดูที่สมาชิกตรงตำแหน่งกลาง array ก่อน (สมมุติว่าดูที่ตำแหน่ง $m = n/2$)
• ถ้า $A[m]$ มีค่าเท่ากับ $x$ ก็ถือว่าจบการทำงานได้ทันที (เจอคำตอบแล้ว)
• ถ้า $A[m]$ มีค่าน้อยกว่า $x$ ดังนั้น เราควรจะหาต่อทางด้านขวาเท่านั้น ไม่ต้องสนใจด้านซ้าย (เพราะด้านซ้ายจะยิ่งมีค่าน้อยลงไปกว่าเดิม) โดยการค้นหาเราจะใช้วิธีแบ่งครึ่งตำแหน่งตรงกลาง array เช่นนี้ไปเรื่อย ๆ
• ถ้า $A[m]$ น้อยกว่า $x$ ก็หาต่อทางด้านซ้ายในทำนองเดียวกัน

หากเปรียบเทียบกับ Linear Search ที่ค่อย ๆ ดูตัวเลขทีละตำแหน่ง Binary Search จะสามารถตัด array ทิ้งออกได้ทีละครึ่งหนึ่งเลยทีเดียว หาก array มีขนาดมากถึง $n=1\,000\,000$ ช่อง ขนาด array จะลดลงจาก $1\,000\,000 \to 500\,000 \to 250\,000 \to \dots \to 1$ (โดยประมาณ) ซึ่งลดลงเพียงแค่ $20$ ครั้งเท่านั้น!

ดังนั้น Time Complexity ของการค้นหาหนึ่งครั้งจึงเป็นเพียงแค่ $\mathcal{O}(\log n)$ เท่านั้น

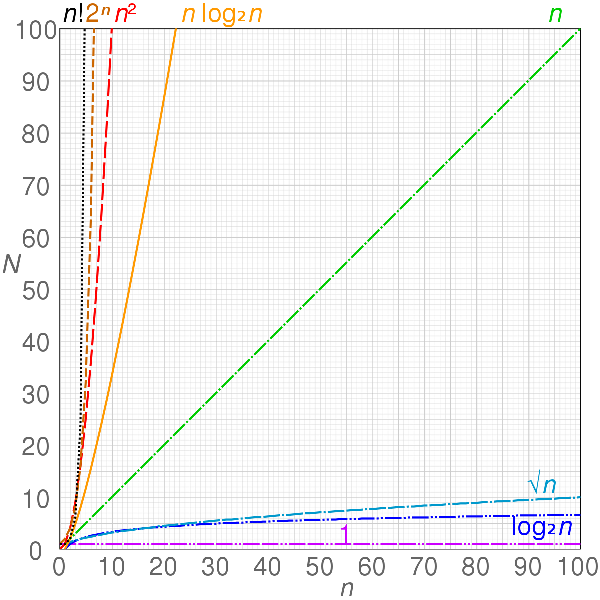
การเปรียบเทียบอัตราการโตของ Time Complexity แต่ละแบบ

อนึ่ง Binary Search จะใช้ได้เฉพาะกรณีที่สมาชิกของ $A$ มีค่าเรียงจากน้อยไปมากเท่านั้น หากยังไม่เรียง เราจำเป็นจะต้องเรียงให้เสร็จก่อนจึงจะใช้ Binary Search ได้ เนื่องจากการเรียงหนึ่งครั้งอาจใช้เวลามากถึง $\mathcal{O}(n \log n)$ เพราะฉะนั้น เราควรจะเรียงเฉพาะกรณีที่มีการถาม-ตอบหลายครั้งเท่านั้น ถ้าถามครั้งเดียวควรใช้ Linear Search แทน (หรืออาจจะหาคำตอบตั้งแต่รับ input สมาชิกของ $A$ เลยก็ได้)

วิธีการเขียนโค้ด Binary Search

สำหรับการเขียนโค้ด Binary Search สามารถเขียนได้สองแบบหลัก ๆ ด้วยกัน คือแบบ Iterative (ใช้ลูปในการค้นหา) และแบบ Recursive (ใช้ recursive function ในการค้นหา)

Iterative Binary Search

ในการเขียนโค้ด Binary Search แบบใช้ลูป จะต้องมีตัวแปร $l$ และ $r$ คอยกำกับว่าตอนนี้สนใจ array ช่วงใดอยู่ (ตอนแรก $l=0$ และ $r=n-1$) แล้วเปรียบเทียบตำแหน่งตรงกลาง ปรับค่า $l$, $r$ ไปเรื่อย ๆ จนกว่าจะเจอตัวเลขที่ต้องการ (หรือหลุดออกลูปเมื่อไม่เจอตัวเลข) ดังนี้

// สมมุติว่า A เรียงจากน้อยไปมากแล้ว
bool binary_search_iterative(int n, int A[], int x) {
    int l = 0, r = n-1;
    while (l <= r) {
        int m = (l+r)/2;
        if (A[m] == x)
            return true;
        else if (A[m] < x) // ถ้าตรงกลางมีค่าน้อยเกิน ควรลองทางด้านขวา (ช่วง [m+1, r])
            l = m+1;
        else // ถ้าตรงกลางมีค่ามากเกิน ควรลองหาทางด้านซ้าย (ช่วง [l, m-1])
            r = m-1;
    }
    return false;
}

กรณีที่ไม่มีค่า $x$ อยู่ใน $A$ สังเกตว่าอัลกอริทึมจะรันจนถึงกรณีที่เหลือสมาชิกตัวเดียว ($l=r$), ทำการเปรียบเทียบ แล้วปรับค่า $l, r$ จนทำให้ $l > r$ นั่นคือ ไม่เหลือช่วงที่ให้ค้นหาอีกแล้ว ทำให้หลุดออกจากลูปแล้ว return false ในที่สุด ดังตัวอย่างข้างล่าง

Recursive Binary Search

นอกจากการใช้ลูปแล้ว ก็สามารถใช้ recursive function ได้ด้วย โดยกำหนดเงื่อนไขในลักษณะเดียวกัน (ใช้ตัวแปร $l$, $r$ กำหนดช่วงของ $A$ ที่สนใจหา แล้ว recursive ปรับไปเรื่อย ๆ)

// สมมุติว่า A เรียงจากน้อยไปมากแล้ว
// binary_search(A, l, r, x) = ค้นหาว่ามีค่า x อยู่ใน A[l..r] หรือไม่
bool binary_search_recursive(int A[], int l, int r, int x) {
    if (l > r) // กรณีที่ l > r เป็นไปไม่ได้อยู่แล้ว ดังนั้นจึงถือว่าไม่มี x
        return false;
    int m = (l+r)/2;
    if (A[m] == x) // หากค่าตรงกลางเป็นค่าที่เราต้องการก็ return ได้เลย
        return true;
    else if (A[m] < x) // หากตรงกลางน้อยไป ให้ลองค้นหาทางด้านขวา
        return binary_search(A, m+1, r, x);
    else // หากตรงกลางน้อยไป ให้ลองค้นหาทางด้านซ้าย
        return binary_search(A, l, m-1, x);
}
// การเรียกใช้ฟังก์ชันตอนแรก ให้ binary_search(A, 0, n-1, x) เพราะเราต้องการให้ค้นหาใน array ทั้งหมด

ทั้งนี้ ถึงแม้การเขียน Binary Search แบบ recursive จะมีความหมายใกล้เคียงกับวิธีที่เราบรรยายเป็นภาษาไทยตอนแรกมากกว่า การใช้ recursive function อาจจะทำให้เสียเวลาในการเรียกฟังก์ชันบ่อยครั้ง และเปลืองหน่วยความจำในการเก็บ function stack ทำให้เกิด stack overflow ได้ (ในกรณีที่ compiler ไม่ optimize tail-call recursion ให้)

ปัญหาที่พบบ่อยในการเขียนโค้ด Binary Search

Binary Search เป็นหนึ่งในอัลกอริทึมที่มีจุดให้โค้ดผิดพลาดหลายจุด ซึ่งอาจจะทำให้คำตอบออกมาผิด หรือโปรแกรมค้าง (ติด infinite loop) ก็ได้

ในกรณีที่เจอบัค วิธีที่ดีที่สุดวิธีหนึ่งคือการปรินท์ค่า $l$, $r$, $m$ ในลูปแต่ละรอบ ทดสอบกับ input ที่เรารู้ว่าผิด จะทำให้เรารู้ว่าฟังก์ชัน binary search ของเราทำงานผิดตั้งแต่ขั้นไหน และผิดอย่างไร (ดูโค้ดที่มาร์ค (*) ข้างล่าง)

บัคที่พบได้บ่อย เช่น

1. ลืมเรียงลำดับสมาชิกของ array $A$
2. กำหนดเงื่อนไขของลูปผิด แทนที่จะเขียน l <= r กลับไปเขียนเป็น l < r แทน ทำให้กรณีที่ $l=r$ (สนใจช่วงสมาชิก 1 ตัว) return false ทันที (ทั้ง ๆ ที่อาจจะ return true ก็ได้ เพราะค่าของ $A$ ที่ตำแหน่ง $l=r$ อาจจะมีค่าเป็น $x$ พอดีก็เป็นไปได้)
3. ลืมใส่วงเล็บตอนคำนวณค่า $m$ ทำให้คำนวณตำแหน่งผิดพลาด เช่น หากสนใจช่วง $[8, 10]$ ควรคำนวณได้ค่า $m=\frac{8+10}{2}=9$ แต่หากโค้ดผิด จะได้ $m=8+\frac{10}{2}=13$ แทน ($13$ อยู่นอกช่วง $[8,10]$ ชัด ๆ)
4. เงื่อนไขเปรียบเทียบผิด หรือกำหนดค่า $l$, $r$ ในแต่ละรอบผิด ทำให้ค้นหา array ผิดช่วง ไม่เจอค่า $x$ ที่ต้องการ
5. ลืม return false ตรงท้ายฟังก์ชัน ถ้าคอมไพล์ผ่าน ผลลัพธ์ที่ return ออกมาอาจจะเป็นค่าขยะ (ทำให้มีโอกาส return ค่า true ออกมาได้)

// (1) A จะต้องมีค่าเรียงจากน้อยไปมาก
bool binary_search_error(int n, int A[], int x) {
    int l = 0, r = n-1;
    while (l < r) { // (2) ต้องแก้เป็น l <= r
        int m = l+r/2; // (3) ต้องใส่วงเล็บ (l+r)/2
        // (*) วิธีการปรินท์ตรวจสอบกรณีที่โค้ด binary search บัค
        printf("l=%d, r=%d | m=%d\n", l, r, m);
        if (A[m] == x)
            return true;
        // (4) เปรียบเทียบผิด ต้องแก้เป็น A[m] < x (หรืออาจจะกำหนดช่วง l, r ด้านล่างผิด)
        else if (A[m] > x)
            l = m+1;
        else
            r = m-1;
    }
    return false; // (5) ลืม return false กรณีที่ไม่เจอ x
}

ตัวอย่างการดัดแปลง Binary Search

หาจำนวนแรกที่มีค่ามากกว่า $x$

ในบางครั้ง โจทย์อาจจะไม่ได้ต้องการให้หาแค่ว่ามีค่า $x$ หรือไม่เพียงอย่างเดียว แต่อาจจะให้หาค่าที่ใกล้เคียง $x$ แทน เช่น ให้หาจำนวนเต็มที่มีค่าที่น้อยที่สุดที่มีค่ามากกว่า $x$ เช่น หาก A = [3, 2, 7, 6, 8] และ $x=5$ จะได้คำตอบเป็น $6$ เพราะ $6$ เป็นตัวแรก (ตัวที่น้อยที่สุด) ที่มีค่ามากกว่า $5$

เช่นเดียวกันกับข้ออื่น ๆ เราควรเรียงสมาชิกของ $A$ จากน้อยไปมากก่อน แล้วควรหาวิธีคิดคำตอบโดยการแบ่งครึ่งในทำนองเดียวกันกับ Binary Search เดิมที่เราเคยทำมา ดังนี้

• สมมุติว่าพิจารณาช่วง $[l, r]$ อยู่ (ตอนแรก $l=0$, $r=n-1$) เราจะดูค่าที่ตำแหน่งตรงกลาง (ตำแหน่ง $m$)
• หาก $A[m] \leq x$ จะสรุปได้ว่าควรพิจารณาช่วงทางด้านขวา ($[m+1, r]$) เพราะสมาชิกในตำแหน่ง $[l, m]$ มีค่าน้อยกว่าหรือเท่ากับ $x$ ทุกตัว แต่โจทย์ต้องการตัวที่มากกว่า $x$
• หาก $A[m] > x$ เราสามารถใช้ตัวที่ $m$ ได้ แต่เนื่องจากว่าอาจจะมีคำตอบที่ดีกว่าอยู่ทางด้านซ้าย ควรลองหาทางด้านซ้ายต่อด้วย ($[l, m-1]$) ส่วนทางด้านขวาไม่ต้องพิจารณา เพราะยังไง ๆ ก็ไม่ใช่ค่าน้อยสุดที่เราหาได้แน่นอน
• สิ้นสุดการทำงานเมื่อ $l > r$ (ไม่เหลือช่วงให้พิจารณาแล้ว)

// สมมุติว่า A เรียงจากน้อยไปมากแล้ว
int first_greater_value(int n, int A[], int x) {
    int l = 0, r = n-1;
    int ans = INT_MAX; // ยังไม่เคยเจอคำตอบ
    while (l <= r) {
        int m = (l+r)/2;
        if (A[m] <= x) {
            l = m+1;
        } else {
            ans = min(ans, A[m]); // จดคำตอบที่ดีที่สุดไว้
            r = m-1;
        }
    }
    return ans;
}

สำหรับโจทย์อื่น ๆ เช่น “หาจำนวนเต็มที่มากที่สุดที่มีค่าน้อยกว่า $x$” สามารถทำได้โดยการคิดอัลกอริทึมทำนองเดียวกัน

หาจุดวิกฤตใน Bitonic Sequence

กำหนดให้ Bitonic Sequence หมายถึงลำดับจำนวนเต็มที่มีค่าเพิ่มขึ้นจนถึงตำแหน่งหนึ่ง แล้วมีค่าลดลงหลังจากนั้นเป็นต้นมา เช่น [1, 4, 5, 7, 8, 6, 5, 3, 2] ถือว่าเป็น Bitonic Sequence (อนึ่ง คำว่าเพิ่มขึ้น/ลดลงในที่นี้ คือ strictly increasing/decreasing ดังนั้น จะต้องไม่มีสมาชิกที่มีค่าเท่ากันอยู่ติดกันเป็นอันขาด) จงหาสมาชิกที่มีค่ามากที่สุด

สำหรับโจทย์ข้อนี้ เราไม่สามารถใช้ Binary Search ได้โดยตรง เพราะสมาชิกตำแหน่งตรงกลางเพียงตัวเดียวไม่สามารถบอกได้ว่าเราควรค้นหาต่อทางด้านซ้ายหรือทางด้านขวา

สังเกตว่าการหาตำแหน่งที่มีค่ามากที่สุด คือการหาตำแหน่งที่มีการเปลี่ยนแปลงจาก “ค่าเพิ่มขึ้น” เป็น “ค่าลดลง” ดังนั้น แทนที่จะสนใจค่าของสมาชิกแต่ละตัว เราจะสนใจการเปลี่ยนแปลงค่าของสมาชิกตัวที่ติดกันแทน ว่ามีค่าเพิ่มขึ้นหรือลดลง

ดังนั้น หาก array $A$ มีสมาชิก $n$ ตัว เราจะสมมุติว่ามี array $B$ โดย $B[i]$ จะมีค่าเป็น false เมื่อ $A[i]<A[i+1]$ (ณ ตำแหน่ง $i$ มีค่าเพิ่มขึ้น) และเป็น true เมื่อ $A[i] > A[i+1]$ (ณ ตำแหน่ง $i$ มีค่าลดลง)

อนึ่ง $B$ เป็น array สมมุติเพื่อความสะดวกในการคิดอัลกอริทึมเท่านั้น นอกจากนี้ array $B$ จะมี index $i = 0$ ถึง $i = n-2$ เท่านั้น (เพราะถ้า $i=n-1$ เราจะไม่สามารถหาค่าของ $A[n]$)

เราสามารถหาตำแหน่งแรกที่มีค่าลดลง (B[i] = true) ได้ดังนี้

• เริ่มต้นพิจารณาช่วง $[l, r]$ (ตอนแรก $l=0$, $r=n-1$) กำหนดให้ $m$ แทนตำแหน่งที่อยู่ตรงกลางระหว่าง $l$, $r$ พอดี
• ถ้า B[m] == false (ตำแหน่ง $i$ มีค่าเพิ่มขึ้น) เราจะไม่สามารถใช้ตำแหน่งนี้ รวมถึงตำแหน่งทางด้านซ้ายทั้งหมด เพราะมีค่าเพิ่มขึ้น เราต้องการตำแหน่งแรกที่มีค่าลดลง เพราะฉะนั้นให้พิจารณาช่วงทางด้านขวาแทน ($[m+1, r]$)
• ถ้า B[m] == true (ตำแหน่ง $i$ มีค่าลดลง) เราสามารถใช้ตำแหน่งนี้ได้ แต่ควรพิจารณาช่วงทางด้านซ้ายด้วย ($[l, m-1]$) เพราะ $m$ อาจจะไม่ใช่ตำแหน่งแรกที่มีค่าลดลงก็ได้ ทั้งนี้สามารถทิ้งช่วงทางด้านขวาไปได้เลย เพราะยังไง ๆ $m$ ย่อมเป็นคำตอบที่ดีกว่าทางด้านขวาแน่นอน
• พิจารณาจนกว่า $l$ จะมีค่ามากกว่า $r$ (ไม่เหลือช่วงให้พิจารณา)

// สมมุติว่า A เป็น bitonic sequence และ n >= 3
int max_in_bitonic(int n, int A[]) {
    int l = 0, r = n-2, ans = -INT_MAX;
    while (l <= r) {
        int m = (l+r)/2;
        if (A[m] < A[m+1]) { // กรณีสมมุติ B[m] == false
            l = m+1;
        } else { // B[m] == true: A[m] เป็นต้นไปมีค่าลดลง
            ans = max(ans, A[m]); // จดคำตอบที่ดีที่สุด (ค่ามากสุด) เอาไว้
            r = m-1;
        }
    }
    return ans;
}

ทั้งนี้ หาก array ที่โจทย์ให้มาเป็นได้ทั้ง bitonic (ขึ้นแล้วลง) และ monotonic (ขึ้นหรือลงอย่างเดียว) ควรนำคำตอบที่ได้จากการ Binary Search ไปเปรียบเทียบกับค่าตรงขอบ array ก่อน ($A[0]$ และ $A[n-1]$) เพราะคำตอบอาจจะอยู่ตรงนั้นก็ได้

การใช้ Binary Search ในการแก้ Optimization Problem

ส่วนใหญ่แล้วโจทย์อัลกอริทึมที่ใช้ในการแข่งขันต่าง ๆ มักจะมีลักษณะเป็น Optimization Problem ซึ่งก็คือโจทย์ที่ต้องการให้หาคำตอบที่ดีที่สุด (เช่น รางวัลมากสุด ค่าใช้จ่ายน้อยสุด ฯลฯ)

โจทย์กลุ่มนี้มักจะแก้ได้โดยใช้ Dynamic Programming หรือ Greedy Algorithm แต่ก็มีโจทย์บางข้อที่สามารถใช้อัลกอริทึม Binary Search มาช่วยแก้ได้เช่นกัน โดยจะขอยกตัวอย่างโจทย์ดังนี้

คำอธิบายโจทย์

เรามีสิ่งของอยู่ทั้งหมด $n$ ชิ้น ชิ้นที่ $i$ ($0 \leq i < n$) มีน้ำหนัก $W_i$ กิโลกรัม บรรจุสิ่งของใส่กล่องไม่เกิน $k$ ใบ โดยมีเงื่อนไขคือ 1) สิ่งของต้องมีน้ำหนักรวมกันไม่เกินน้ำหนักมากสุดที่กล่องรับไหวและ 2) หากสิ่งของชิ้นที่ $a$ และชิ้นที่ $b$ อยู่ในกล่องเดียวกัน ($a \leq b$) สิ่งของทุกชิ้นที่อยู่ระหว่างสองชิ้นนี้ (ทุกชิ้นที่ $i$ ที่ $a < i < b$) จะต้องอยู่ในกล่องนี้ด้วย (นั่นคือสิ่งที่ของในกล่องเดียวกันจะต้องเป็นสิ่งของที่ตำแหน่งติดกัน) ถ้าทุกกล่องสามารถรับน้ำหนักได้เท่ากัน จงหาว่าเราสามารถใช้กล่องที่ทนทานน้อยสุดเท่าใด โดยที่ยังบรรจุของตามเงื่อนไขได้

ตัวอย่าง หาก W = [6, 2, 4, 3, 7] และมีกล่อง $k=3$ ใบ กล่องจะต้องรับน้ำหนักได้อย่างน้อย $8$ กิโลกรัมจึงจะสามารถบรรจุของใส่กล่องได้ตามเงื่อนไข (แบ่งบรรจุดังนี้: [6,2], [4,3], [7]) เพราะถ้ากล่องบรรจุได้แค่ $7$ กิโลกรัม จะต้องใช้กล่องอย่างน้อย $4$ ใบจึงจะบรรจุได้ ([6], [2,4], [3], [7]) ซึ่งเกินจำนวนกล่องที่กำหนดไว้แค่ $3$ ใบ ดังนั้น คำตอบน้อยสุดที่เป็นไปได้คือ $8$ กิโลกรัม

ข้อสังเกตเกี่ยวกับโจทย์

การหาคำตอบที่น้อยที่สุดนั้นอาจจะทำได้ยาก เพราะฉะนั้น เราควรลองเปลี่ยนปัญหาให้ง่ายขึ้น อาจจะทำให้สังเกตอะไรได้สะดวกขึ้น

“สมมุติว่าเรารู้น้ำหนักที่กล่องรับได้อยู่แล้ว เราจะตรวจสอบได้อย่างไรว่า เราสามารถบรรจุสิ่งของด้วยน้ำหนักกล่องนี้ได้ตามเงื่อนไข และใช้กล่องไม่เกิน $k$ ใบ”

หากเราสามารถแปลงปัญหาให้อยู่ในรูป Decision Problem หรือปัญหาการตัดสินใจเช่นนี้แล้ว ให้คิดว่าจะมีวิธีการตรวจสอบอย่างไร

สำหรับโจทย์ข้อนี้ เราสามารถลองบรรจุของได้ ดังนี้

• เราจะใช้กล่องใบเดียวก่อน แล้วบรรจุสิ่งของทีละชิ้น (ตั้งแต่ชิ้นที่ $i=0$ เป็นต้นไป) จนกว่าจะไม่สามารถบรรจุได้ เพราะถ้าบรรจุแล้วน้ำหนักจะเกิน
• หากบรรจุไม่ได้ ให้เปลี่ยนมาใช้กล่องใบถัดไป และบรรจุเช่นนี้เรื่อย ๆ จนกว่าจะบรรจุสิ่งของครบทุกชิ้น (ถือว่าทำสำเร็จ) หรือใช้กล่องเกิน $k$ ใบก่อน (ถือว่าทำไม่ได้)

สังเกตว่าวิธีนี้จะใช้กล่องน้อยที่สุดเท่าที่เป็นไปได้ เพราะเรานำสิ่งของใส่กล่องเดิมตลอดเท่าที่เป็นไปได้ (หากยังใส่ได้อยู่ ไม่ควรเปิดกล่องใหม่เพราะจะเป็นการใช้กล่องโดยสิ้นเปลือง) ดังนั้น การตรวจสอบว่าทำได้หรือทำไม่ได้ด้วยวิธีนี้ย่อมให้ผลถูกต้อง

ข้อสังเกตอีกอย่างหนึ่งที่สำคัญคือ ยิ่งน้ำหนักที่กล่องรับได้เพิ่มขึ้น จำนวนกล่องที่จะเป็นต้องใช้ก็จะลดลงเรื่อย ๆ ดังนั้น เราสามารถ binary search หาน้ำหนักที่น้อยที่สุดที่เป็นไปได้ ที่ทำให้จำนวนกล่องไม่เกิน $k$ โดยหากพิจารณาช่วงน้ำหนัก $[l, r]$ แล้วทดลองน้ำหนัก $m$ ไป พบว่าได้ $x$ กล่อง ถ้า $x > k$ (ใช้กล่องเกินที่กำหนด) จะต้องลองเพิ่มน้ำหนักขึ้น (พิจารณาช่วง $[m+1, r]$) แต่หาก $x \leq k$ ให้จดคำตอบไว้ แล้วลองบีบน้ำหนักให้น้อยลง (พิจารณา $[l, m-1]$)

Implementation

ในการเขียนโค้ด ควรจะแยกฟังก์ชันเพื่อคำนวณจำนวนกล่องเมื่อกำหนดจำนวนสิ่งของ ออกจากส่วนที่เป็นการ binary search หาคำตอบ เพื่อให้สะดวกต่อการอ่านหรือ debug

// หาจำนวนกล่องน้อยสุดที่ต้องใช้เมื่อกล่องรับน้ำหนักได้ cap kg
int package(int n, int W[], int cap) {
    int box_count = 1, current_sum = 0;
    for (int i = 1; i <= n; ++i) {
        // กรณีที่มีสิ่งของขนาดมากเกินกล่อง 1 กล่อง ไม่สามารถ pack ได้แน่นอน
        // (โค้ดไม่ควรเข้ากรณีนี้ เพราะ cap น่าจะ >= สิ่งของที่หนักที่สุดอยู่แล้ว)
        if (W[i] > cap)
            return INT_MAX;
        // กรณีที่ไม่สามารถเพิ่มใส่กล่องใบปัจจุบันได้แล้ว ให้เริ่มกล่องใหม่
        if (current_sum+W[i] > cap) {
            ++box_count;
            current_sum = 0;
        }
        // นำของใส่กล่อง
        current_sum += W[i];
    }
    return box_count;
}

// หาน้ำหนักรับได้ของกล่องน้อยสุดที่ต้องใช้ ถ้ามีกล่องไม่เกิน k กล่อง
int find_min_capacity(int n, int W[], int k) {
    // หาน้ำหนักกล่องน้อยสุดที่อาจเป็นไปได้ (รับสิ่งของชิ้นที่หนักที่สุดได้พอดี)
    // และน้ำหนักมากสุดที่เป็นไปได้ (รับสิ่งของได้ทั้งหมด)
    int max_w = 0, sum = 0;
    for (int i = 0; i < n; ++i) {
        max_w = max(max_w, W[i]);
        sum += W[i];
    }
    // binary search
    int l = max_w, r = sum, ans = sum;
    while (l <= r) {
        int m = (l+r)/2;
        // หากกำหนดน้ำหนัก = m แล้วใช้กล่องมากเกิน k ใบ ต้องลองเพิ่มน้ำหนัก
        if (package(n, W, m) > k) {
            l = m+1;
        } else { // หากใช้กล่อง <= k ใบ ให้ลองบีบน้ำหนักให้น้อยลงอีก
            ans = min(ans, m); // จดน้ำหนักน้อยสุดที่ทำได้ไว้
            r = m-1;
        }
    }
    return ans;
}

Time Complexity

ในการทดลองบรรจุแต่ละครั้ง เราจำเป็นต้องลูปทดลองบรรจุของแต่ละชิ้นเป็นจำนวนทั้งหมด $\mathcal{O}(n)$ ชิ้น และคำนวณผลรวม/จำนวนกล่องเพียงเท่านั้น ดังนั้น เวลารวมในการทดลองบรรจุสิ่งของจึงเป็น $\mathcal{O}(n)$ ต่อครั้ง

เราทำการ binary search บนค่าน้ำหนักที่กล่องรับไหว ซึ่งมีค่าได้มากสุดเท่ากับผลรวมของน้ำหนักสิ่งของทั้งหมด แต่ละครั้งเราจำเป็นต้องเรียกฟังก์ชัน package เพื่อลองบรรจุสิ่งของ ดังนั้น Time Complexity รวมจึงเป็น $\mathcal{O(n \log S})$ เมื่อ $S$ เท่ากับผลรวมของน้ำหนักสิ่งของทั้งหมด

อนึ่ง หากไม่ต้องการโค้ดส่วนที่หาค่า $l$, $r$ เริ่มต้น สามารถทำได้โดยกำหนดให้ $l=1$, $r=$ ค่าใหญ่ ๆ ที่มากกว่า $S$ แน่นอน (ปกติโจทย์จะกำหนดขอบเขตมาให้ว่าสมาชิกแต่ละตัวมีค่ามากสุดเท่าใด) แล้วรันอัลกอริทึมตามปกติ ทั้งนี้ time complexity จะขึ้นอยู่กับค่า $r$ เริ่มต้นที่กำหนดไว้แทน

บทสรุป

หลังจากที่เขียนบล็อกอย่างยืดยาวมาเป็นเวลาหลายชั่วโมง บวกกับทำ visualization เพื่อฝึกสกิลการเขียนเว็บ (ซึ่งตอนนี้กากมาก D:) ก็หวังว่าจะบทความนี้จะช่วยให้ทุกคนเข้าใจเรื่อง Binary Search รวมถึงเอาประยุกต์ใช้ทำโจทย์อัลกอริทึมต่าง ๆ ได้นะครับ

:D