หลาย ๆ คนอาจจะเคยได้ยินมาบ้างว่า Dynamic Programming (DP) เป็นหนึ่งในเนื้อหาที่เข้าใจยากที่สุดสำหรับนักเรียน/นักศึกษาที่ศึกษาเกี่ยวกับ Algorithms และ Data Structures ทั้งนี้อาจจะเป็นเพราะ

• หลาย ๆ คนยังไม่คุ้นเคยกับการใช้ Recursion มากนัก ตัวอย่างต่าง ๆ ที่เคยเรียนมาก็มักจะเป็นแค่โจทย์ง่าย ๆ อย่างการคำนวณเลข Factorial, Fibonacci แต่แทบจะไม่ได้แตะอะไรที่ซับซ้อนกว่านั้น อย่างเช่นการแก้ปัญหา N-Queen, Knapsack ฯลฯ ด้วย Recursive Backtracking

• ยังไม่ชินกับการคิดแบบ abstract หรือแบบ general (เกี่ยวโยงกับ Recursion โดยตรง) และไม่ค่อยคุ้นเคยกับคณิตศาสตร์เลยรู้สึกว่า DP ยาก

• เริ่มต้นมาโจทย์ DP ส่วนใหญ่ เราไม่สามารถแก้เองได้ ต้องอาศัยการอ่านเท่านั้น และทำไปเรื่อย ๆ ดัดแปลงไปเรื่อย ๆ ฝึกไปจนกว่าจะเก่ง แต่หลายคนไม่ได้มีเวลามากขนาดนั้น

และเหตุผลอื่น ๆ อีกมากมายนับไม่ถ้วน

สำหรับบทความนี้ ผมก็อยากจะลองอธิบายเกี่ยวกับเรื่อง Dynamic Programming ดูบ้าง ไม่รู้ว่าจะต่างจากที่อื่นอย่างไร แต่อย่างน้อยก็หวังว่าจะเป็นอีกวิธีที่ทำให้แต่ละคนศึกษาเรื่อง Dynamic Programming ได้เข้าใจมากขึ้นละกันนะครับ :)

Table of Contents

• Dynamic Programming คืออะไร?
• วิธีการแก้ปัญหาด้วย Dynamic Programming
• ตัวอย่างที่ 1: Coin Change Problem
• ตัวอย่างที่ 2: Number of Paths in 2D grid
• ข้อสังเกตเกี่ยวกับการกำหนดสูตร DP
• ตัวอย่างที่ 3: Maximum Sum Subarray
• ตัวอย่างที่ 4: Longest Increasing Subsequence (LIS)
• บทสรุป

Dynamic Programming คืออะไร?

Those who cannot remember the past are condemned to repeat it.

George Santayana

Dynamic Programming (DP) เป็นเทคนิคหนึ่งสำหรับแก้ปัญหาที่ซับซ้อน โดยการแก้ปัญหาย่อย (ปัญหาที่มีขนาดเล็กลงมา) ตั้งแต่ปัญหาขนาดย่อยที่สุดขึ้นมาก่อน แล้วค่อย ๆ เพิ่มขอบเขตขึ้นมาจนถึงปัญหาที่มีขนาดใหญ่ที่สุด

เนื่องจากตัว ปัญหาย่อย (Subproblem) ที่แก้เป็นปัญหาที่มีลักษณะเหมือนกัน แค่มีข้อมูลให้จัดการน้อยกว่า ดังนั้นวิธีการแก้ปัญหา DP มักจะต้องแก้ด้วย recursive function หรือไม่ก็ต้องใช้สูตรคณิตศาสตร์ทีมีลักษณะเป็นสมการเวียนเกิด (recurrence formula)

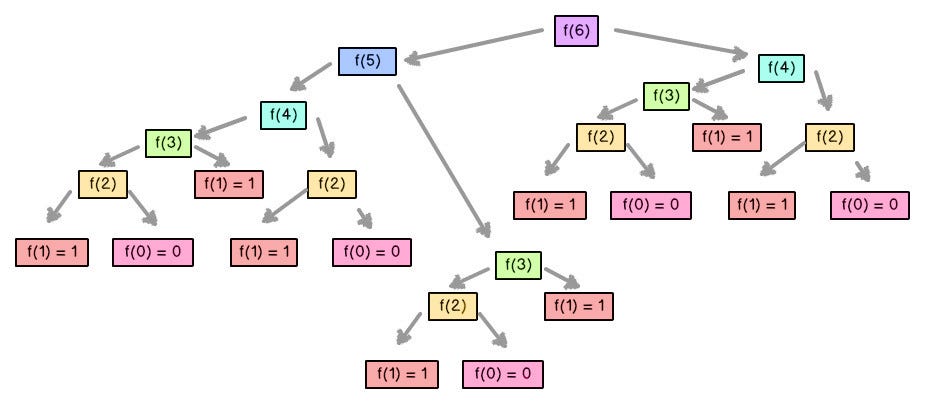
การคิดคำนวณเลขฟีโบนักชี (Fibonacci Number) ด้วย recursive function แบบธรรมดา

สำหรับโจทย์ส่วนใหญ่แล้ว ตัวปัญหาย่อยจะมีลักษณะดังนี้

• ปัญหาย่อยที่ซ้อนทับกัน (Overlapping Subproblem) นั่นคือ เมื่อย่อยขนาดปัญหาใหญ่มาเป็นปัญหาย่อยแล้ว จะพบว่าได้ปัญหาย่อยเหมือนกันซ้ำกันมาก หากเราจดคำตอบไว้ (memoization) ก็จะทำให้เราไม่ต้องเสียเวลาคิดซ้ำ ๆ

• โครงสร้างย่อยที่เหมาะสมที่สุด (Optimal Substructure) หากคำตอบของปัญหาใหญ่เป็นคำตอบที่ดีที่สุด ตัวคำตอบของปัญหาย่อยก็ต้องดีที่สุดตามไปด้วย ดังนั้น ในการแก้โจทย์ เราทราบเพียงแค่คำตอบที่ดีที่สุดของปัญหาย่อยแต่ละปัญหาย่อย แล้วเลือกนำมาดัดแปลงเพิ่มเติมเป็นคำตอบของปัญหาใหญ่ก็พอแล้ว ไม่ต้องเก็บทุกคำตอบที่เป็นไปได้

วิธีการแก้ปัญหาด้วย Dynamic Programming

ในการแก้ปัญหา DP จะมีขั้นตอนที่สามารถนำมาใช้แก้ได้ คือ

1. กำหนดปัญหาให้ชัดเจน (กำหนดเป็นฟังก์ชันว่าต้องรับข้อมูลอะไร และ return ข้อมูลอะไร ให้เอื้อกับการทำ recursive function)

2. หาคำตอบของปัญหาใหญ่จากปัญหาย่อย

3. เขียนสูตรออกมาในรูปทั่วไป (เขียน recurrence formula และกำหนด base case)

4. วิเคราะห์ Time Complexity และ Space Complexity

5. Implement! ทำได้สองวิธีคือ Top-down Approach และ Bottom-up Approach

ตัวอย่างที่ 1: Coin Change Problem

กำหนดให้คุณมีเงินอยู่ทั้งหมด $n$ บาท ต้องการหาว่าจะต้องใช้เหรียญ $1$ บาท, $3$ บาท, $4$ บาท น้อยสุดจำนวนกี่เหรียญ

สำหรับโจทย์ข้อนี้ เราไม่สามารถแก้ด้วย Greedy Algorithm ซึ่งก็คือการที่เราพยายามเลือกเหรียญที่มีมูลค่ามากที่สุดมาใช้เรื่อย ๆ จนกว่าจะได้เงินที่เราต้องการ เช่น หากเราต้องการเงิน $18$ บาท ก็สามารถทำได้โดยการหยิบเหรียญ $4$ บาทจำนวน $4$ เหรียญ (รวมเป็น $16$ บาท) ตามด้วยหยิบเหรียญ $1$ บาทอีก $2$ เหรียญ (ครบ $18$ บาทพอดี)

เพราะว่าวิธีนี้ไม่ได้คำตอบที่ดีที่สุดเสมอไป ยกตัวอย่าง หากเราต้องการเงิน $6$ บาท วิธี Greedy จะต้องใช้ $3$ เหรียญ ($4+1+1$) แต่คำตอบที่ดีที่สุดคือใช้ $2$ เหรียญ ($3+3$) ใช้วิธีนี้ไม่ได้ >:(

ลองแก้ปัญหานี้ด้วย Dynamic Programming โดยทำตามขั้นตอน

ขั้นที่ 1: กำหนดปัญหาให้ชัดเจน

กำหนดให้ฟังก์ชัน int change(int i) เป็นฟังก์ชันที่แก้ปัญหาดังกล่าว โดยจำนวนเต็ม $i$ ที่รับมาแทนจำนวนเงินที่ต้องการ (สังเกตว่า $i$ อาจจะมีค่าไม่เท่ากับ $n$ ก็ได้) ส่วนค่าที่ return คือจำนวนเหรียญที่น้อยที่สุดที่ต้องใช้

ขั้นที่ 2: หาคำตอบของปัญหาใหญ่จากปัญหาย่อย

สำหรับข้อนี้ สังเกตว่ามีปัญหาที่มีลักษณะคล้ายกันแต่มีขนาดเล็กกว่า เช่น หากเราต้องการเงิน $18$ บาท เราอาจจะลองดูกรณีทั้งหมดที่เป็นไปได้ของคำตอบขั้นแรกพอ ซึ่งในกรณีนี้จะทำได้ 3 แบบก็คือ

• ทอนเหรียญ $1$ บาทไปก่อน ส่วนอีก $17$ บาทที่เหลือถือว่าเป็นปัญหาย่อย (สังเกตว่าเป็นปัญหาเดียวกันเลข แค่เลขน้อยลง)

• ทอนเหรียญ $3$ บาทไปก่อน ส่วนอีก $16$ บาทที่เหลือถือว่าเป็นปัญหาย่อย

• ทอนเหรียญ $4$ บาทไปก่อน ส่วนอีก $14$ บาทที่เหลือถือว่าเป็นปัญหาย่อย

เลขอื่น ๆ ก็สามารถคิดในทำนองนี้ได้เช่นกัน

ขั้นที่ 3: เขียนสูตรออกมาในรูปทั่วไป

การแก้ปัญหานี้ หากมีเงิน $i$ บาท จะหาจำนวนเหรียญน้อยที่สุดที่ต้องใช้ได้จาก 3 กรณีคือ

• ทอนเหรียญ $1$ บาทไปก่อน 1 เหรียญ บวกกับจำนวนเหรียญที่ต้องใช้ทอนเงิน $i-1$ บาทที่เหลือ

• ทอนเหรียญ $3$ บาทไปก่อน 1 เหรียญ บวกกับจำนวนเหรียญที่ต้องใช้ทอนเงิน $i-3$ บาทที่เหลือ

• ทอนเหรียญ $4$ บาทไปก่อน 1 เหรียญ บวกกับจำนวนเหรียญที่ต้องใช้ทอนเงิน $i-4$ บาทที่เหลือ

ซึ่งเราต้องการเลือกวิธีที่ทำให้จำนวนเหรียญน้อยสุด ดังนั้น change(i) จะมีค่าเท่ากับ 1 + min{change(i-1), change(i-3), change(i-4)} (เหรียญแรกที่ใช้ บวกกับจำนวนเหรียญที่ใช้ทอนเงินที่เหลือหลังจากเหรียญแรก)

นอกจากนี้ ต้องกำหนด base case

• กรณีที่ $i = 0$ คำตอบจะเป็น 0 เพราะทอนเงิน 0 บาทไม่จำเป็นต้องใช้สักเหรียญ

• กรณีที่ $i < 0$ เป็นไปไม่ได้ แต่เนื่องจากสูตรที่เราใช้ หากไม่ได้ป้องกันไว้ อาจจะคำนวณมาถึงตรงนี้ได้ (เช่น การคิดค่าของ change(2) อาจจะมีการทอนเหรียญ $3$ บาท ทำให้เหลือเงิน $-1$ บาท) ดังนั้นจะต้องกำหนดคำตอบเป็น infinity (จำนวนใหญ่ ๆ) เพื่อให้เวลานำไปคิดในสูตร $\min$ จะถูกมองข้ามไป เพราะคำตอบมีขนาดใหญ่เกินไป

ขั้นที่ 4: วิเคราะห์ Time Complexity และ Space Complexity

เนื่องจากว่าปัญหาย่อยอาจมีได้มากถึง $\mathcal{O}(n)$ ปัญหา (ตั้งแต่ change(1) ถึง change(n)) และแต่ละปัญหาย่อย เราคิดเพียงครั้งเดียวเท่านั้น แต่ละครั้งใช้เวลา $\mathcal{O}(1)$ (พิจารณาเพียงแค่ 3 กรณีเท่านั้น ใช้เวลาคงที่) Time Complexity ของวิธีนี้จึงเป็น $\mathcal{O}(1)$

เนื่องจากว่าต้องเก็บคำตอบทั้งหมด $\mathcal{O}(n)$ กรณี จึงมี Space Complexity เป็น $\mathcal{O}(n)$

ขั้นที่ 5: Implement

การ Implement สูตร DP ที่เราได้มาสามารถทำได้สองวิธีหลัก ๆ ด้วยกัน

• Top-down Approach เป็นการ implement recursive function โดยตรง แล้วใช้ array หรือ data structure อื่น ๆ (เช่น map) ในการจำคำตอบ (memoization) กรณีที่เคยคิดคำตอบกรณีนั้นมาแล้ว

• Bottom-up Approach เป็นการแก้ปัญหาด้วยการลูปธรรมดา โดยแก้ปัญหากรณีเล็ก ๆ ก่อนที่จะขึ้นมาปัญหากรณีใหญ่

ตัวอย่างโค้ด Top-down Approach

การเขียนโค้ด Top-down Approach ทำได้โดยการเขียน recursive function ตรง ๆ เลย เพียงแค่เติมในส่วนของ memo เข้าไปช่วยในการจำคำตอบกรณีที่อาจจะมีการคิดซ้ำ ๆ เท่านั้น (เช่น กรณีที่เหลือเงิน $i = 1, 2, 3$ บาทอาจจะถูกคิดคำนวณซ้ำ ๆ บ่อยเกิน เป็นต้น)

int memo[MAX_N]; // initially set all to -1 to mark as "not done yet"

int change(int i) {
    // base cases:
    if (i == 0) return 0;
    if (i < 0) return 1e9; // 1e9 = 1,000,000,000
    // already solved cases:
    if (memo[i] != -1)
        return memo[i];
    
    // recursive step:
    int ans = 1 + min(change(i-1), min(change(i-3), change(i-4)));
    memo[i] = ans; // memoize the answer
    return ans;
}

// cout << change(6) << endl;
// result = 2

ตัวอย่างโค้ด Bottom-up Approach

แทนที่จะเขียนเป็นฟังก์ชัน recursive ก็ลองลูปหาคำตอบตั้งแต่กรณีที่ต้องการจำนวนเงินแค่ $i=1$ บาท, $i=2$ บาท, ขึ้นมาจนถึง $i=n$ บาท ดังนี้

int ans[MAX_N];
ans[0] = 0; // base case

for (int i = 1; i <= n; ++i) {
    ans[i] = 1e9; // don't know a way to solve yet
    if (i-1 >= 0) // try using 1-baht coin if possible
        ans[i] = min(ans[i], 1+ans[i-1]);
    if (i-3 >= 0) // try using 3-baht coin if possible
        ans[i] = min(ans[i], 1+ans[i-3]);
    if (i-4 >= 0) // try using 4-baht coin if possible
        ans[i] = min(ans[i], 1+ans[i-4]);
}

cout << change(n) << endl;
// if n = 6, result = 2

สังเกตว่าในการเขียนแบบ Bottom-up เราไม่สามารถใช้ base case เป็นกรณีที่ $i < 0$ ได้ ดังนั้นจึงต้องใช้วิธีการ if ป้องกันไม่ให้เผลอเข้าถึงกรณีนั้นแทน

ตัวอย่างที่ 2: Number of Paths in 2D grid

สังเกตว่าในตัวอย่างแรก ข้อมูลที่กำหนดมาให้มีเพียงแค่จำนวนเงินที่ต้องการเท่านั้น แต่ DP สามารถใช้แก้โจทย์ที่มีการกำหนดข้อมูลอื่น ๆ ได้ด้วย

กำหนดตารางขนาด $n \times m$ มาให้ โดยแต่ละช่องมีค่าเป็น . (เดินผ่านได้) หรือ # (มีสิ่งกีดขวาง) จงนับจำนวนวิธีเดินจากมุมบนซ้าย (ตำแหน่ง $(1, 1)$) มาถึงมุมล่างขวา (ตำแหน่ง $(n, m)$) โดยอนุญาตให้เดินลงหรือขวาเท่านั้น (ห้ามเดินขึ้นหรือซ้าย)

เช่น กรณีที่มีตารางขนาด $5 \times 4$ ดังนี้

.....
.#...
...#.
...#.

จะมีวิธีเดินทั้งหมด 3 วิธีด้วยกัน ได้แก่

xxxxx   xxxx.   xxx..
.#..x   .#.xx   .#xxx
...#x   ...#x   ...#x
...#x   ...#x   ...#x

เช่นเดียวกัน โจทย์ข้อนี้ เราสามารถทดลองแก้ด้วย Dynamic Programming ได้โดยการใช้ขั้นตอน ดังนี้

ขั้นที่ 1: กำหนดปัญหาให้ชัดเจน

ลองมองว่าตารางที่กำหนดให้เป็น array 2 มิติใน global scope ส่วนตัวปัญหาที่เราต้องการจะแก้ เราจะไม่จำกัดแค่การเดินจาก $(1, 1)$ ไป $(n, m)$ อย่างเดียว แต่เดินไปยังจุด $(i, j)$ ใด ๆ ก็ได้

เราก็จะสามารถกำหนดฟังก์ชัน int count_paths(int i, int j) ขึ้นมาโดย $i$ และ $j$ กำหนดจุดเป้าหมายที่ต้องการเดินไป ส่วนค่าที่ return คือจำนวนวิธีทั้งหมดที่เป็นไปได้

ตามตัวอย่างข้างบน count_paths(5, 4) จะต้องมีค่าเท่ากับ $3$ ส่วน count_paths(1, 2) จะต้องมีค่าเท่ากับ $1$ เป็นต้น

ขั้นที่ 2: หาคำตอบของปัญหาใหญ่จากปัญหาย่อย

สังเกตว่า ถ้าเราต้องการทราบวิธีการเดินไปยังจุด $(i, j)$ จะสามารถทำได้สองวิธีใหญ่ ๆ ด้วยกัน

• เดินจากจุด $(1, 1)$ มายัง $(i-1, j)$ ให้ได้ก่อน แล้วค่อยเดินลงมาอีกก้าว มาถึง $(i, j)$ พอดี

• เดินจากจุด $(1, 1)$ มายัง $(i, j-1)$ ให้ได้ก่อน แล้วค่อยเดินขวาอีกก้าว มาถึง $(i, j)$ พอดี

ดังนั้น จำนวนวิธีก็จะได้จากทั้งสองรูปแบบบวกกัน

ขั้นที่ 3: เขียนสูตรออกมาในรูปทั่วไป

เมื่อคิดได้ดังข้างบนแล้ว สูตรก็ค่อนข้างจะชัดเจน: count_paths(i, j) จะมีค่าเท่ากับ count_paths(i-1, j) + count_paths(i, j-1)

ทั้งนี้ต้องระวังกรณีพิเศษต่าง ๆ ได้แก่

• กรณีที่ $i < 1$ หรือ $j < 1$ ให้ถือว่าคำตอบเท่ากับ $0$ (ตามเงื่อนไข เราไม่สามารถเดินขึ้น/ซ้ายจากจุด $(1, 1)$ ไปยังจุดพวกนี้ได้)

• กรณีที่ตำแหน่ง $(i, j)$ เดินผ่านไม่ได้ (เป็นสัญลักษณ์ #) ให้ถือว่าคำตอบเป็น $0$ ไปโดยปริยาย (ไม่ต้องใช้สูตรคิด) เพราะเดินมาถึงจุดนี้ไม่ได้

• กรณีที่ $(i, j) = (1, 1)$ ให้ถือว่าคำตอบเท่ากับ $1$ ได้เลย

ขั้นที่ 4: วิเคราะห์ Time Complexity และ Space Complexity

เนื่องจากว่าปัญหาย่อยอาจมีได้มากถึง $\mathcal{O}(nm)$ ปัญหา และแต่ละปัญหาย่อย เราคิดเพียงครั้งเดียวเท่านั้น แต่ละครั้งใช้เวลา $\mathcal{O}(1)$ Time Complexity ของวิธีนี้จึงเป็น $\mathcal{O}(nm)$

เนื่องจากว่าต้องเก็บคำตอบทั้งหมด $\mathcal{O}(nm)$ กรณี จึงมี Space Complexity เป็น $\mathcal{O}(nm)$

ขั้นที่ 5: Implement

Top-down Approach

เนื่องจากว่า argument ของฟังก์ชันมีมากถึงสองตัว เราต้องใช้ array 2 มิติในการจดคำตอบที่อาจจะเคยทำซ้ำ

char A[MAX_N][MAX_M]; // assume the board's data is in A[1.n][1..m]
int dp[MAX_N][MAX_M]; // initially set all to -1 to mark as "not done yet"

int count_paths(int i, int j) {
    if (i < 1 || j < 1)
        return 0;
    if (A[i][j] == '#')
        return 0;
    if (i == 1 && j == 1)
        return 1;
    
    if (dp[i][j] != -1) // if already done this case
        return dp[i][j];
    // otherwise, calculate and remember then return
    dp[i][j] = count_paths(i-1, j) + count_paths(i, j-1);
    return dp[i][j];
}

// according to the above example:
// cout << count_paths(5, 4) << endl;
// result = 3

Bottom-up Approach

ในกรณีที่มี argument ของฟังก์ชันมากกว่า 1 ตัว เราต้องคิดให้ดี ๆ ว่าจะเริ่มทำจากตำแหน่งไหนก่อน จึงจะคำนวณไม่ผิดพลาด ปัญหาที่อาจเกิดขึ้น เช่น

• หากเลือกคำนวณตำแหน่ง $(3, 3)$ ก่อนตำแหน่ง $(3, 2)$ จะมีปัญหา เพราะเรายังไม่ทราบคำตอบ ณ ตำแหน่ง $(3, 2)$

สำหรับข้อนี้ วิธีที่ง่ายที่สุดคือการคิดไปทีละแถว

• คิดตั้งแต่ $(1, 1)$ ไปจนถึง $(1, m)$ ให้เสร็จก่อน

• แล้วค่อยทำ $(2, 1)$ ไปจนถึง $(2, m)$

• ทำไปเรื่อย ๆ จนถึงแถวสุดท้าย (แถวที่ $n$)

char A[MAX_N][MAX_M]; // assume the board's data is in A[1..n][1..m]
int dp[MAX_N][MAX_M]; // set everything to 0 (so dp[0][0..m] and dp[0..n][0] will be 0)

for (int i = 1; i <= n; ++i) {
    for (int j = 1; j <= m; ++j) {
        if (A[i][j] == '#')
            dp[i][j] = 0;
        else if (i == 1 && j == 1)
            dp[i][j] = 1;
        else
            dp[i][j] = dp[i-1][j] + dp[i][j-1];
    }
}

// according to the above example:
// cout << dp[5][4] << endl;
// result = 3

ข้อสังเกตเกี่ยวกับการกำหนดสูตร DP

ในขั้นแรกของการทำโจทย์ DP เราจะต้องนิยามปัญหาให้เหมาะสมกับการทำเป็น recursive function เพราะหากเรานิยามผิด ก็อาจจะไม่สามารถหาสมการเวียนเกิดที่หาคำตอบได้ถูกต้อง หรือหาได้แต่สมการที่ใช้เวลาในการคำนวณนาน

argument ของปัญหาย่อยที่เราพยายามกำหนดนั้น เรามักจะเรียกว่า state ซึ่งก็คือสถานะของการคำนวณนั่นเอง เช่น ในตัวอย่างที่ 1 อาจมองได้ว่า change(i) แสดงถึงการที่เราทอนเหรียญได้จนเหลือเงินที่ต้องการทอนเพิ่มอีก $i$ บาท เป็นต้น

ในตัวอย่างที่ 3 และ 4 จะแสดงให้เห็นว่าบางครั้งเราอาจจะกำหนด state เพื่อหาคำตอบแบบตรงไปตรงมาไม่ได้

ตัวอย่างที่ 3: Maximum Sum Subarray

กำหนดจำนวนเต็มให้ทั้งหมด $n$ ตัว (อาจมีค่าติดลบได้) จงหา subarray (ช่วงย่อยหนึ่งช่วงของ array) ที่มีผลรวมมากที่สุด

เช่น กรณีที่ array เป็น [-2, 3, 2, -1, 4, -9, 3] ผลรวมที่มากที่สุดที่เป็นไปได้คือ $8$ เกิดจากช่วงที่มีข้อมูล [3, 2, -1, 4]

ขั้นที่ 1: กำหนดปัญหาให้ชัดเจน

ก่อนอื่น กำหนดให้ array ของตัวเลขดังกล่าวเป็น array A[1..n] ที่อยู่ใน global scope

นิยามแบบที่ 1

หากเราพยายามกำหนดฟังก์ชัน int max_sum(int i) เพื่อหาว่าคำตอบที่ดีที่สุดเมื่อพิจารณาเพียงแค่ array A[1..i] เมื่อคำนวณเสร็จ max_sum(1), max_sum(2), …, max_sum(n) แล้ว เราจะได้คำตอบอยู่ที่ max_sum(n) พอดี

แต่เราไม่สามารถคิดสมการเวียนเกิดได้แบบง่าย ๆ เพราะหากพยายามคิดค่าของ max_sum(i) ตามนิยามนี้ จะต้องพิจารณาสองกรณี

• คำตอบอาจจะเกิดจาก max_sum(i-1) เลยก็ได้ (สมาชิกตัวที่ $i$ ที่เพิ่มมาไม่ได้ทำให้คำตอบเปลี่ยน)

• มิเช่นนั้น คำตอบอาจจะเกิดจากช่วงที่สิ้นสุด ณ ตำแหน่ง $i$ พอดี ซึ่งมีได้มากถึง $i$ ช่วง (ช่วง A[1..i], A[2..i], ..., A[i..i])

แต่กรณีที่ 2 จะต้องใช้เวลาในการลูปมากสุดถึง $\mathcal{O}(n)$ และเนื่องจากเราต้องคิด max_sum(1..n) รวม $\mathcal{O}(n)$ ครั้ง เวลาการทำงานทั้งหมดจึงเป็น $\mathcal{O}(n^2)$ ซึ่งไม่ได้ดีกว่าวิธี Brute Force เลย

นิยามแบบที่ 2

ลองกำหนดเป็นฟังก์ชัน int max_sum_ending(int i) แทน เพื่อหาว่าคำตอบที่ดีที่สุดเมื่อพิจารณาเพียงแค่ subarray ที่จบที่ตำแหน่ง $i$ พอดี คือเท่าใด

หากกำหนดเป็นเช่นนี้แล้ว คำตอบสุดท้ายจะไม่ได้อยู่ที่ max_sum_ending(n) เพียงอย่างเดียว เพราะคำตอบอาจจะเป็น subarray ที่จบที่ตำแหน่งใดก็ได้ ดังนั้น คำตอบจะเท่ากับ max(max_sum_ending(1), max_sum_ending(2), ..., max_sum_ending(n))

หากใช้นิยามนี้ การหาคำตอบ max_sum_ending(i) สามารถทำได้จากการพิจารณาสองกรณี

• คำตอบอาจจะเกิดจากการใช้ค่า ณ ตำแหน่ง $n$ โดด ๆ เพียงตัวเดียวเลย นั่นก็คือ มีค่าเท่ากับ A[i]

• คำตอบอาจจะเกิดจากการนำคำตอบที่ดีที่สุดที่จบที่ตำแหน่ง $n-1$ แล้วเอา A[i] เพิ่มต่อเข้าไป ทำให้คำตอบเป็น max_sum_ending(i-1)+A[i]

สังเกตว่า กรณีที่สองเราไม่จำเป็นต้องลูปอีกแล้ว เพราะเรามีข้อมูลจาก max_sum_ending(i-1) อยู่แล้วว่าถ้าต้องการให้ subarray จบที่ตำแหน่ง $n-1$ จะได้คำตอบมากสุดเท่าใด สิ่งที่เหลืออยู่ก็เพียงแค่นำ A[i] เพิ่มเข้าไปต่อท้ายเท่านั้น

ขั้นที่ 2: หาคำตอบของปัญหาใหญ่จากปัญหาย่อย

ทำไปข้างบนแล้ว :D

ขั้นที่ 3: เขียนสูตรออกมาในรูปทั่วไป

ค่าของ max_sum_ending(i) หาได้ดังนี้

• ถ้า $i=1$ คำตอบจะเท่ากับ A[1]

• ถ้า $i>1$ คำตอบจะเท่ากับ max(A[i], max_sum_ending(i-1)+A[i])

ขั้นที่ 4: วิเคราะห์ Time Complexity และ Space Complexity

เนื่องจากว่าปัญหาย่อยอาจมีได้มากถึง $\mathcal{O}(n)$ ปัญหา และแต่ละปัญหาย่อย เราคิดเพียงครั้งเดียวเท่านั้น แต่ละครั้งใช้เวลา $\mathcal{O}(1)$ Time Complexity ของวิธีนี้จึงเป็น $\mathcal{O}(n)$

เนื่องจากว่าต้องเก็บคำตอบทั้งหมด $\mathcal{O}(n)$ กรณี จึงมี Space Complexity เป็น $\mathcal{O}(n)$

ขั้นที่ 5: Implement

เนื่องจากว่าเราต้องคิดคำตอบจาก max(max_sum_ending(1), max_sum_ending(2), ..., max_sum_ending(n)) อยู่แล้ว การเขียน Top-down Approach ในข้อนี้ค่อนข้างจะเสียเวลา เพราะยังไง ๆ เราก็ต้องสร้างคำตอบจากกรณี $i = 1$ จนถึง $i = n$ ครบทั้งหมด ดังนั้นจึงควร implement แบบ Bottom-down แทน

int A[MAX_N];
int dp[MAX_N]; // dp[0] = 0

int ans = -1e9;
for (int i = 1; i <= n; ++i) {
    dp[i] = max(A[i], dp[i-1]+A[i]);
    ans = max(ans, dp[i]);
}

cout << ans << endl;
// if A[1..n] = [-2, 3, 2, -1, 4, -9, 3]
// cout << ans << endl;
// result = 8

ตัวอย่างที่ 4: Longest Increasing Subsequence (LIS)

กำหนดลำดับจำนวนเต็มความยาว $n$ ตัวมาให้ จงหา increasing subsequence (ลำดับย่อยที่ตัวเลขเรียงจากน้อยไปมาก) ที่มีความยาวมากที่สุด

คำว่า subsequence ในที่นี้ หมายถึงการเลือกสมาชิกเพียงแค่บางตัวของ array ไว้โดยยังคงลำดับเดิมอยู่ (แต่ไม่จำเป็นต้องอยู่ติดกัน)

หาก array ที่กำหนดให้คือ [10, 22, 9, 33, 21, 50, 41, 60, 80] ลำดับย่อยที่เรียงจากน้อยไปมากที่ยาวที่ยาวที่สุดคือ [10, 22, 33, 50, 60, 80] (ความยาว $6$ ตัว)

ขั้นที่ 1: กำหนดปัญหาให้ชัดเจน

เช่นเดียวกับตัวอย่างที่ 3 เราไม่สามารถกำหนดฟังก์ชัน int LIS(int i) ได้ เพราะหากกำหนดเช่นนี้แล้ว กรณีที่ต้องคิดมีสองแบบคือ

• คำตอบเท่ากับ A[i] เพียงตัวเดียวเลย

• คำตอบมีค่าเท่ากับ LIS(i-1) (เพิ่ม A[i] เข้ามาก็ไม่ได้ช่วยอะไร)

• ต้องนำ A[i] ไปต่อท้ายลำดับที่ยาวที่สุดก่อนหน้า แต่เนื่องจากว่าเราไม่ทราบว่าลำดับที่ยาวที่สุดใน LIS(i-1) จบด้วยเลขอะไร จึงไม่สามารถนำมาต่อได้ เพราะอาจจะผิดเงื่อนไข “เรียงจากน้อยไปมาก”

ดังนั้น สำหรับข้อนี้ เพื่อให้เราสามารถทราบได้ตลอดว่าตัวเลขตัวสุดท้ายคือเลขอะไร เราจะต้องเปลี่ยนมาใช้ฟังก์ชัน int LIS_end(int i) แทน เพื่อค้นหา Longest Increasing Subsequence ที่จบที่ตำแหน่ง $i$ พอดี

คำตอบของทั้งลำดับ ก็จะได้จาก max{LIS_end(1), LIS_end(2), ..., LIS_end(n)}

ขั้นที่ 2: หาคำตอบของปัญหาใหญ่จากปัญหาย่อย

หากต้องการให้ LIS มาจบที่ตำแหน่ง $n$ พอดีสามารถทำได้สองวิธี

• ใช้ A[i] เพียงแค่ตัวเดียวเลย (ความยาว $1$ ตัว)

• นำ A[i] ไปต่อกับ LIS ที่จบที่ตำแหน่ง $1$ ถึง $n-1$ แต่ว่าตำแหน่งที่นำมาต่อนั้น ต้องมีค่าน้อยกว่า A[i] (เพราะต้องการให้เรียงจากน้อยไปมาก)

ขั้นที่ 3: เขียนสูตรออกมาในรูปทั่วไป

(กำหนดให้ LIS_end(i) มีค่าเท่ากับ dp[i])

หากต้องการให้ลำดับจบที่ $i$ จะต้องเลือกว่าตัวก่อนหน้า A[i] จะเป็นตำแหน่งใด — หากได้ตำแหน่ง $j$ มา ก็จะทำให้ความยาวทั้งหมดเท่ากับ (ความยาวของลำดับจนถึงตำแหน่ง $j$) + (ตำแหน่ง $i$ เพิ่มอีก $1$ ตำแหน่ง)

ถ้าเลือกต่อกับตัวก่อนหน้าไม่ได้สักตัว คำตอบก็จะมีค่าเท่ากับ 1 (นั่นก็คือ ลำดับมีแค่ตัวที่ $i$ เพียงตัวเดียว)

ขั้นที่ 4: วิเคราะห์ Time Complexity และ Space Complexity

เนื่องจากว่าปัญหาย่อยอาจมีได้มากถึง $\mathcal{O}(n)$ ปัญหา และแต่ละปัญหาย่อย เราคิดเพียงครั้งเดียวเท่านั้น แต่ละครั้งใช้เวลา $\mathcal{O}(n)$ (ลูปเพื่อเลือกว่าจะเอาไปต่อกับลำดับใด) Time Complexity ของวิธีนี้จึงเป็น $\mathcal{O}(n^2)$

เนื่องจากว่าต้องเก็บคำตอบทั้งหมด $\mathcal{O}(n)$ กรณี จึงมี Space Complexity เป็น $\mathcal{O}(n)$

ขั้นที่ 5: Implement

int A[MAX_N]; // assume data is in A[1..n]
int dp[MAX_N];

int ans = 0;
for (int i = 1; i <= n; ++i) {
    dp[i] = 1;
    for (int j = 1; j < i; ++j) {
        if (A[j] < A[i])
            dp[i] = max(dp[i], 1+dp[j]);
    }
    ans = max(ans, dp[i]);
}

cout << ans << endl;

บทสรุป

ในบทความนี้ พูดถึงเพียงแค่หลักการในการแก้โจทย์คร่าว ๆ พร้อมทั้งตัวอย่างเพียงแค่ 4 ตัวอย่าง แต่หวังว่าตัวอย่างที่ยกมาจะช่วยให้เข้าใจคอนเซปต์เรื่อง Dynamic Programming มากขึ้น

ถึงอย่างไรก็ตาม ในการทำโจทย์จริง ๆ แล้ว จะต้องใช้การฝึกฝนเป็นอย่างมาก หากต้องการเข้าใจเรื่องนี้อย่างถ่องแท้ แนะนำให้ลองศึกษา Classical Problem อื่น ๆ ดู หรือลองหาโจทย์ DP นั่งคิดดู

Classical Problems ที่น่าสนใจ เช่น

• Maximum Independent Sum

• 0–1 Knapsack Problem

• Longest Common Subsequence

• Matrix Chain Multiplication

• Rod Cutting

• Text Justification

• Egg Dropping

ขอให้สนุกกับการแก้โจทย์ DP ครับ :D