aqua-ified thoughts

never developed nor fully solidified

ตะลุยโจทย์ Graph ระดับโหดใน Competitive Programming

Monday, August 19, 2019, 02:30 AM
Tutorial, Programming, Algorithms and Data Structures

ส่วนใหญ่แล้วโจทย์กราฟที่เราพบในการแข่งขันต่าง ๆ หรือพวกโจทย์สัมภาษณ์ มักจะเป็นโจทย์ที่ประยุกต์ใช้ Graph Algorithms บน input graph ตรง ๆ เช่น

  • Depth-first Search/Breadth-first Search สำหรับท่องกราฟ
  • Dijkstra’s Algorithm สำหรับหา Single-source Shortest Path
  • Kruskal’s Algorithm สำหรับหา Minimum Spanning Tree

โจทย์บางข้ออาจจะซับซ้อนกว่านั้น เพราะ input ไม่ได้กำหนดกราฟมาให้ แต่เราต้องมองให้ออกเองว่าเราสามารถแปลงข้อมูลที่โจทย์ให้มาเป็นกราฟแล้วใช้พวก algorithm ที่มีอยู่แก้

ในบทความนี้ ผมก็จะขอยกตัวอย่างโจทย์กราฟซับซ้อนบางข้อเพื่อเป็นแนวทางให้กับคนที่สนใจเข้าร่วมการแข่งขันอัลกอริทึมต่าง ๆ หรืออยากจะฝึกฝน problem-solving skill เพิ่มเติมครับ :)

Table of Contents

ข้อที่ 1: Knight on a Chessboard

Problem Statement

สมมุติว่ามีตารางหมากรุกขนาด $n \times m$ แต่ละช่องของตารางอาจจะเป็นช่องปกติ หรือช่องที่ห้ามเข้าถึง

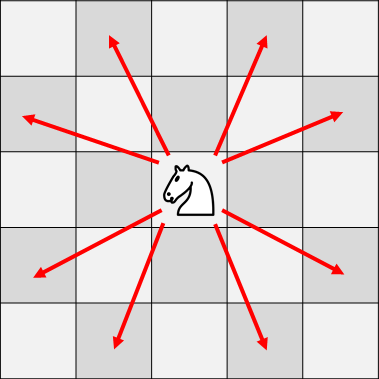
เรามี Knight 1 ตัววางอยู่ที่ตำแหน่ง $(s_x, s_y)$ จงหาว่าเราสามารถเคลื่อนย้าย Knight ตัวนี้ไปยังตำแหน่ง $(t_x, t_y)$ ได้ด้วยการกระโดดน้อยสุดทั้งหมดกี่ครั้ง การกระโดดของ Knight เป็นดังภาพ

รูปแบบการเดินของ Knight

Knight ห้ามกระโดดออกนอกตาราง หรือกระโดดไปยังช่องที่ห้ามเข้าถึงเป็นอันขาด

Solution Idea

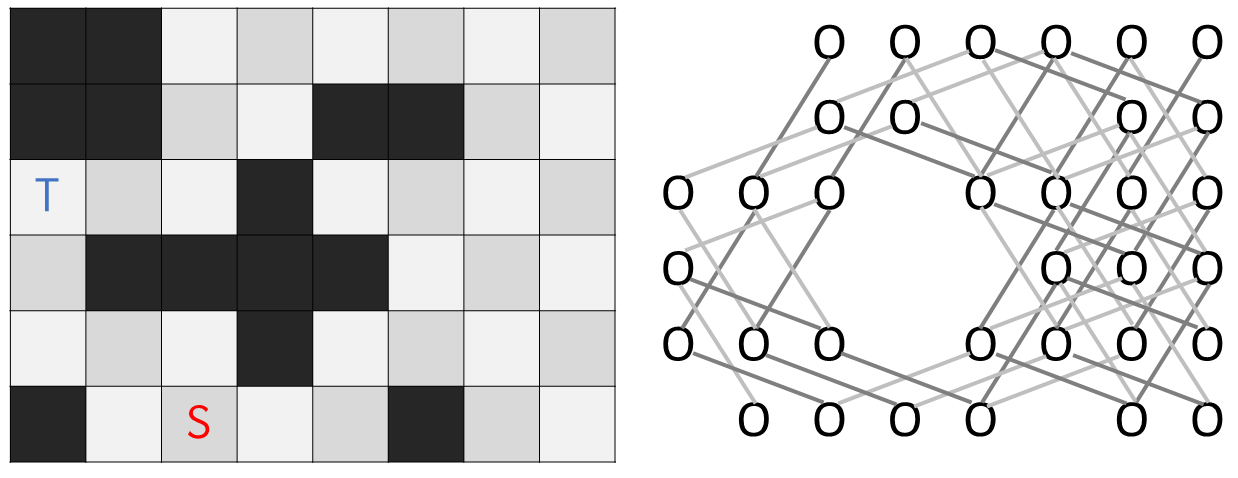
หากเราสังเกตดี ๆ จะเห็นว่า เราสามารถมองว่าตารางที่กำหนดให้เป็นกราฟ โดยที่มีเส้นเชื่อมระหว่าง node ระบุถึงการเดินทางทั้งหมดที่เป็นไปได้ของ Knight ดังตัวอย่าง

ตัวอย่างการสร้างกราฟจากตารางที่กำหนดให้

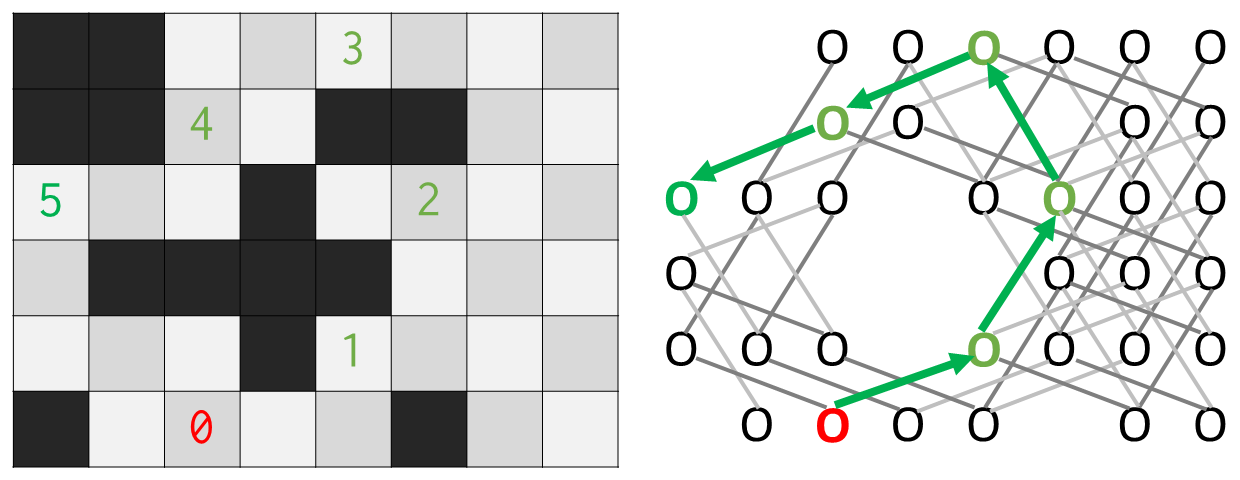
เมื่อเห็นเช่นนี้แล้ว การหาจำนวนครั้งกระโดดน้อยสุดจากตำแหน่ง $(s_x, s_y)$ ไปยัง $(t_x, t_y)$ ก็ไม่ต่างอะไรกับการหาเส้นทางสั้นสุดจาก node $(s_x, s_y)$ ไปยัง node $(t_x, t_y)$

เนื่องจากเส้นเชื่อมทุกเส้นของกราฟมีน้ำหนักเท่ากัน (เพราะการกระโดดทุกแบบนับเป็นกระโดด 1 ครั้งเท่ากันหมด) เราจึงสามารถแก้โจทย์ดังกล่าวได้ด้วยอัลกอริทึม Breadth-first Search

การหาเส้นทางสั้นสุดจากกราฟที่สร้างขึ้น

Complexity Analysis

ในกรณีแย่สุด BFS จะต้องท่องผ่านทุกจุดและทุกเส้นเชื่อม กราฟที่เรากำหนดขึ้นมามีจุดทั้งหมด $nm$ จุด และมีละจุดมีเส้นเชื่อมออกจากจุดนั้นประมาณ 8 เส้น จึงสรุปได้ว่าวิธีนี้มี Time Complexity และ Space Complexity เป็น $\mathcal{O}(nm)$

Solution Code 1

ข้อที่ 2: Shortest Path with Fee Waiver

Problem Statement

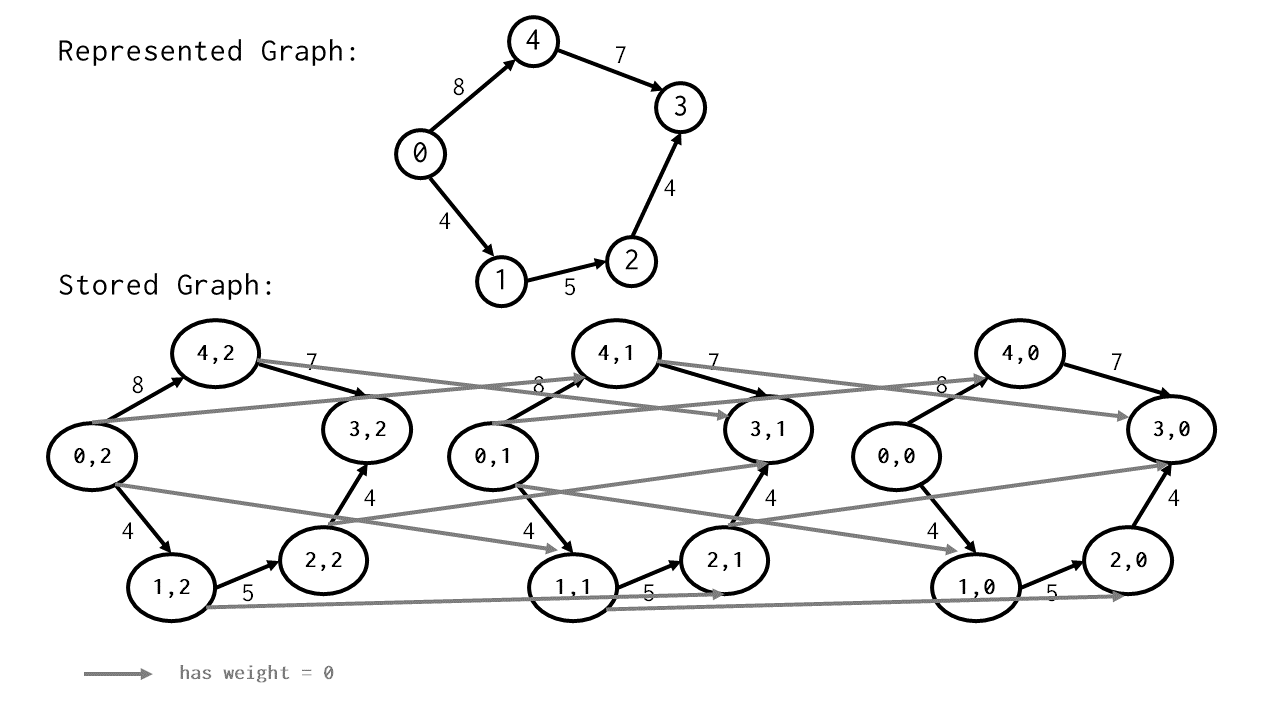
กำหนดกราฟระบุทิศทาง ระบุน้ำหนัก (directed, weighted graph)

  • มี node ทั้งหมด $n$ node
  • มี $m$ edge โดย edge ที่ $i$ เชื่อมจาก node $u_i$ ไป $v_i$ และมีค่าใช้จ่ายในการเดินทาง (น้ำหนัก) เท่ากับ $w_i$

หากเรามีสิทธิ์ในการเดินผ่าน edge โดยไม่เสียค่าใช้จ่ายได้ไม่เกิน $k$ เส้น จงหาว่าเราสามารถเดินทางจาก node $s$ ไปยัง node $t$ ได้โดยใช้ค่าใช้จ่ายน้อยสุดเท่าใด

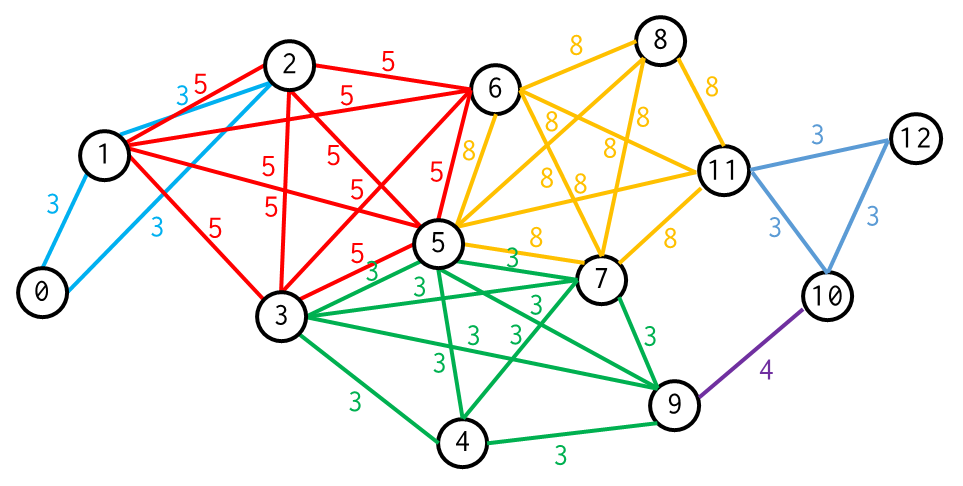
กรณีตัวอย่างสำหรับโจทย์ข้อที่ 2

Solution Idea

ตามที่โจทย์กำหนด ชัดเจนอยู่แล้วว่าจะต้องใช้อัลกอริทึมสำหรับหาเส้นทางสั้นสุดอย่าง Dijkstra’s Algorithm แน่ ๆ แต่เราไม่สามารถทำบนกราฟนี้ได้ได้ตรง ๆ เพราะเงื่อนไขพิเศษของโจทย์ข้อนี้ (สามารถเดินผ่านเส้นเชื่อมได้ฟรี ๆ $k$ ครั้ง)

วิธีหนึ่งที่จะช่วยให้สามารถแก้โจทย์จำพวกนี้ได้ง่ายขึ้นคือการกำหนดสถานะการทำงาน/การเดินทาง/ฯลฯ (state) ขึ้นมาให้สัมพันธ์กับโจทย์ และสังเกตว่าการเปลี่ยนสถานะทั้งหมดที่เป็นไปได้ มีอะไรบ้าง

เช่น สำหรับข้อนี้ เราอาจจะกำหนดสถานะเป็นคู่อันดับ $(u, f)$ เพื่อแสดงให้เห็นว่า “ตอนนี้เราอยู่ node หมายเลขอะไร” และ “สามารถใช้สิทธิ์เดินผ่าน edge ฟรีได้อีกกี่ครั้ง”

หากเราอยู่ที่ node $u$ สิ่งที่เราทำได้คือการเลือกว่าจะเดินไปยัง node ใดที่ติดอยู่กับ $u$ ต่อ (ตามกราฟที่โจทย์กำหนดให้มาใน input) สมมุติว่าเลือกไปยัง node $v$ โดยเส้นเชื่อมมีน้ำหนัก $w$ เราสามารถเลือกได้ว่า

  • จะเดินทางจาก node $u$ ไป node $v$ โดยเสียค่าใช้จ่ายตามปกติ ดังนั้น จะเป็นการเปลี่ยนสถานะจาก $(u, f) \to (v,f)$ โดยมีค่าใช้จ่ายเท่ากับ $w$ หรือ
  • จะเดินทางจาก node $u$ ไป node $v$ โดยใช้สิทธิ์เดินผ่านฟรี 1 ครั้ง ดังนั้น จะเป็นการเปลี่ยนสถานะจาก $(u,f) \to (v,f-1)$ โดยมีค่าใช้จ่ายเท่ากับ $0$ (วิธีนี้สามารถเลือกได้เมื่อ $f \geq 1$ เท่านั้น ถ้า $f=0$ คือหมดสิทธิ์แล้ว ห้ามใช้การเปลี่ยนสถานะนี้)

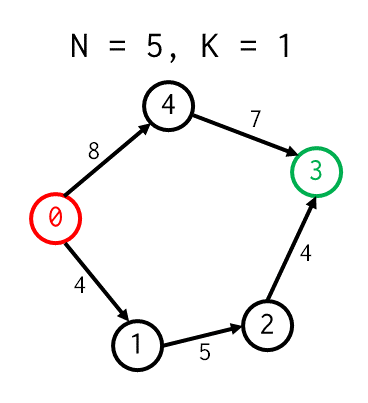
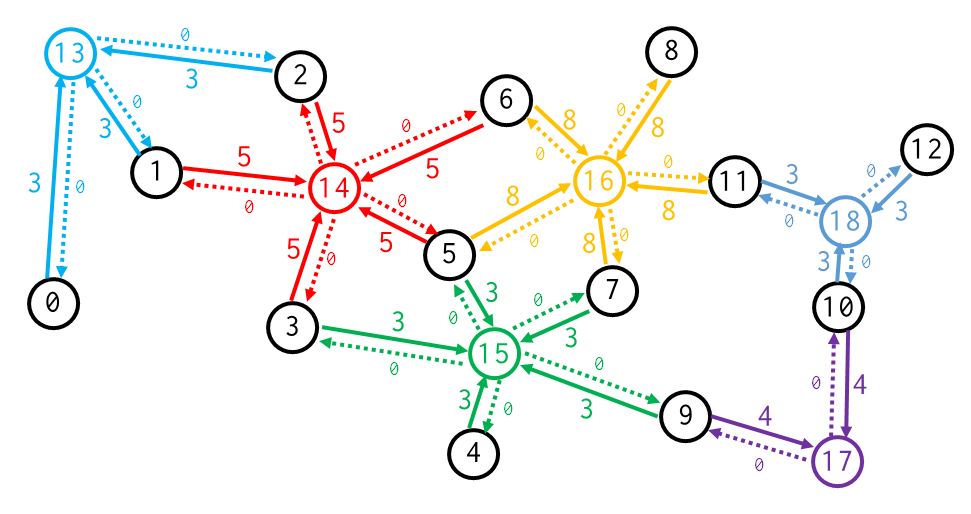
ตัวอย่างการสร้าง State Graph จากกราฟเดิมที่กำหนดให้

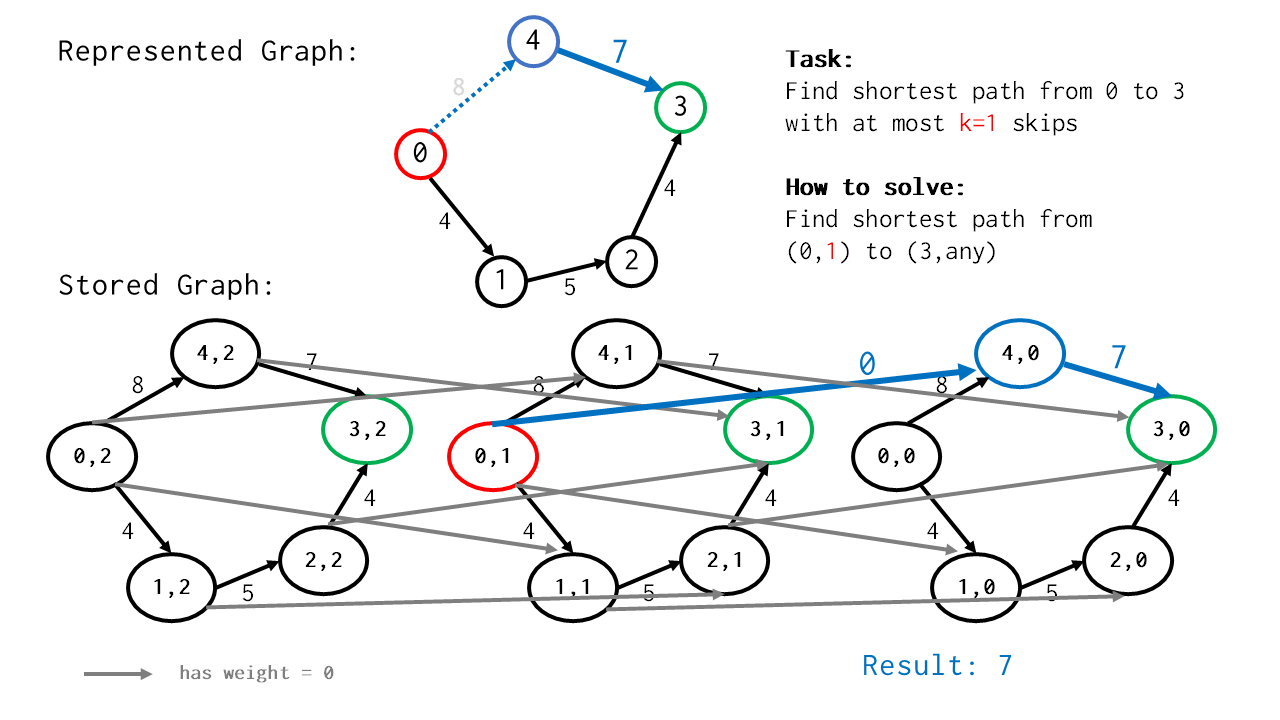
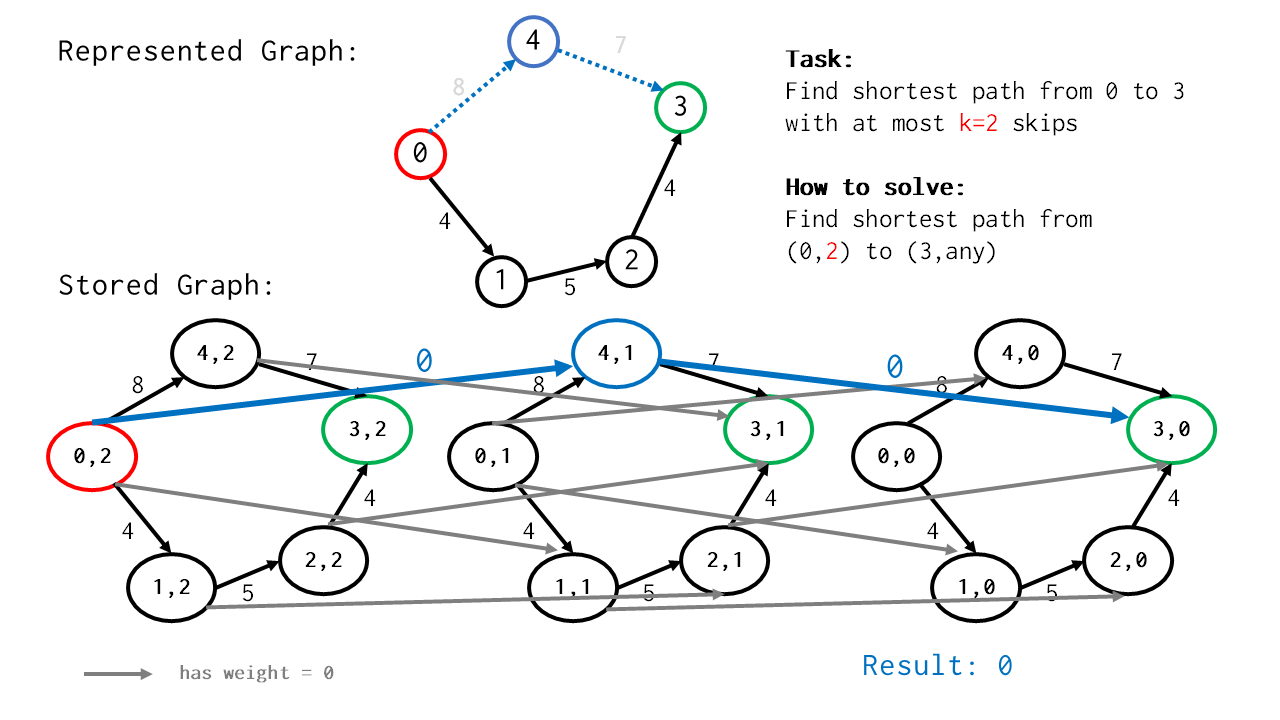
เมื่อกำหนดสถานะได้เช่นนี้แล้ว การแก้โจทย์เดิมของเราสามารถทำได้โดย หาลำดับการเปลี่ยนสถานะที่เสียค่าใช้จ่ายน้อยที่สุด จากสถานะเริ่มต้น “อยู่ที่ node $s$ และเหลือสิทธิ์ $k$ สิทธิ์” ไปยังสถานะสิ้นสุด “อยู่ที่ node $t$ แต่เหลือสิทธิ์เท่าใดก็ได้ (สมมุติว่าเหลือ $i$ สิทธิ์)”

หรือก็คือ การหาเส้นทางสั้นสุดบนกราฟสถานะ จากสถานะ $(s,k)$ ไปยังสถานะ $(t,?)$ ใด ๆ นั่นเอง

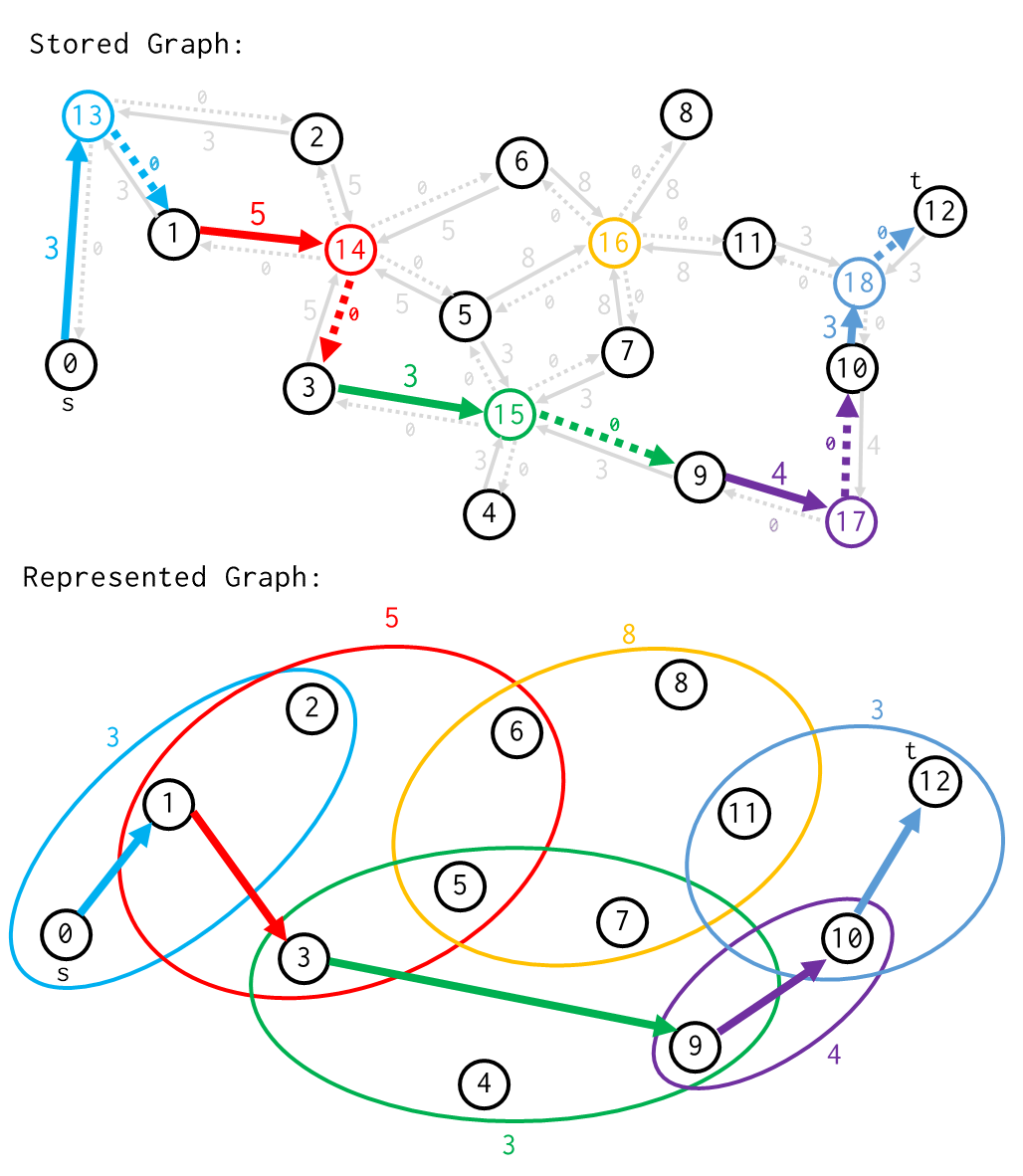
การหาเส้นทางสั้นสุดจาก $s = 0$ ไป $t = 3$ โดยอนุญาตให้ข้ามเส้นได้ $k = 1$ เส้น

การหาเส้นทางสั้นสุดจาก $s = 0$ ไป $t = 3$ โดยอนุญาตให้ข้ามเส้นได้ $k = 2$ เส้น

Complexity Analysis

ถึงแม้ว่ากราฟดั้งเดิมของเราจะมี $n$ node $m$ edge ก็จริง แต่วิธีการแก้ปัญหาของเราจริง ๆ แล้วทำบนกราฟสถานะ (state graph) ที่เรากำหนดขึ้นมา ดังนั้นการวิเคราะห์ Time/Space Complexity จะต้องวิเคราะห์จากจำนวน node/edge บนกราฟสถานะดังกล่าว

  • วิธีของเรา สถานะขึ้นอยู่กับ node ที่อยู่และจำนวนสิทธิ์ที่เหลืออยู่ ดังนั้นจำนวนสถานะทั้งหมดคือ $\mathcal{O}(nk)$
  • จากแต่ละสถานะของเรา จะสามารถเปลี่ยนสถานะได้ตามจำนวน node ที่ติดอยู่กับ node ปัจจุบันคูณ 2 (เลือกใช้สิทธิ์/ไม่ใช้สิทธิ์เดินฟรี) ดังนั้น รวม ๆ แล้ว ถ้ากราฟมี $m$ node จำนวนเส้นเชื่อมสถานะจะอยู่ที่ประมาณ $\mathcal{O}(mk)$

หาก implement Dijkstra’s Algorithm โดยใช้ priority_queue ปกติแล้ว Time Complexity จะเป็น $\mathcal{O}(|E|+|V|\log|V|)$ ดังนั้น วิธีที่เราใช้แก้ข้อนี้จึงมี Time Complexity รวมเป็น $\mathcal{O}(mk + nk \log nk)$ นั่นเอง

หากโจทย์ข้อนี้เป็นโจทย์การแข่งขัน ถ้า Time Limit เป็น 1 วินาที ก็จะมี constraint อยู่ที่ประมาณ $n \leq 10^5$, $m \leq 10^5$ และ $k \leq 10$

Solution Code 2

ข้อที่ 3: Hypergraph Traveling

Problem Statement

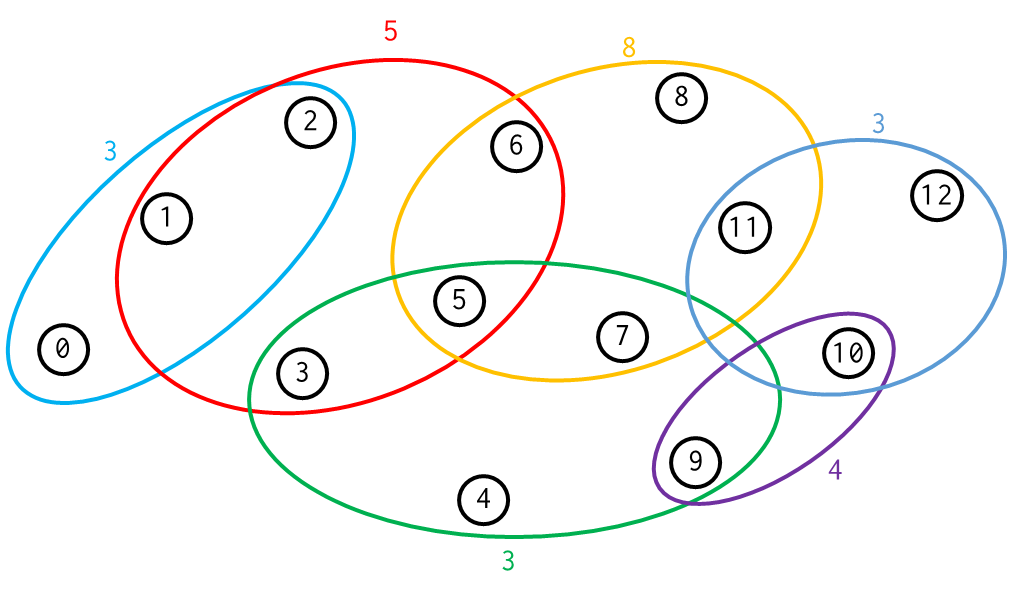
กำหนดกราฟที่มี $n$ node $m$ hyperedge มาให้ โดยที่ hyperedge คือเส้นเชื่อมที่ไม่ได้เชื่อมเพียงแค่ 2 node เท่านั้น อาจจะเชื่อมหลาย node ก็ได้ หากเราอยู่ที่ node ใด node หนึ่งของ hyperedge เราก็สามารถเลือกเดินทางไปยัง node อื่นที่เชื่อมด้วย hyperedge นี้ได้โดยเสียค่าใช้จ่ายเท่ากับน้ำหนักของ hyperedge นี้ จงหาเส้นทางสั้นสุดจาก node $s$ ไปยัง node $t$

กรณีตัวอย่างสำหรับโจทย์ข้อที่ 3

Solution Idea

Naive Approach

วิธีหนึ่งที่ง่ายที่สุดในการแก้โจทย์ข้อนี้ก็คือการแปลง hyperedge กลับเป็น edge ปกติ โดยสร้างเส้นเชื่อมระหว่างทุกคู่ node ใน hyperedge ดังภาพ

ตัวอย่างการสร้างกราฟตาม Naive Approach

ในกรณีที่มี hyperedge ที่เชื่อมระหว่างทุก node ในกราฟ วิธีการสร้างกราฟแบบนี้จะต้องสร้าง edge มากถึง $\mathcal{O}(n^2)$ ดังนั้น วิธีนี้ไม่เหมาะสมสำหรับการแก้โจทย์ข้อนี้

Better Approach

อีกวิธีหนึ่งที่เราทำได้คือ สำหรับแต่ละ hyperedge ให้สร้าง node พิเศษขึ้นมา 1 node แล้วสร้าง edge เชื่อมจาก node ในกลุ่มมายัง node พิเศษ น้ำหนักเท่ากับค่าใช้จ่ายในการใช้ hyperedge แล้วสร้าง edge เชื่อมจาก node พิเศษนี้กลับไป node ในกลุ่มด้วยน้ำหนัก 0

หากสร้างกราฟเช่นนี้ แต่ละ node จะไม่สามารถเดินทางหากันโดยตรงได้อีกต่อไป แต่จะต้องเดินทางผ่าน node พิเศษ เป็นตัวกลางในการเคลื่อนที่ของ hyperedge นั้น ๆ ดังภาพ

วิธีการสร้างกราฟโดยใช้ dummy node แทน hyperedge แต่ละกลุ่ม

เมื่อสร้างกราฟนี้ได้แล้วก็สามารถหาเส้นทางสั้นสุดได้ทันที

การหาเส้นทางสั้นสุดโดยใช้กราฟที่สร้างขึ้น

Complexity Analysis

เช่นเดียวกับข้อก่อนหน้า การวิเคราะห์ Time/Space Complexity จะต้องวิเคราะห์จากจำนวน node (จำนวนสถานะ) และจำนวน edge (การเปลี่ยนสถานะ) ของกราฟที่เราสร้างขึ้นมาใหม่ ดังนี้

  • กำหนดให้ hypergraph ที่โจทย์กำหนดให้มี $n$ node, $m$ hyperedge นอกจากนี้ กำหนดให้จำนวน node ที่ hyperedge แต่ละเส้นเชื่อมเข้าด้วยกัน รวมแล้วมีทั้งหมด $k$ node
  • กราฟใหม่ที่เราสร้างขึ้นมาจะมี $n+m$ node ($n$ node ปกติ และ $m$ node พิเศษสำหรับแต่ละ hyperedge)
  • เส้นเชื่อมที่สร้างจะมีทั้งหมด $2k$ เส้น (แต่ละ hyperedge มีเส้นเชื่อมไปยัง node ในกลุ่มสองทิศทาง)

หากใช้ Dijkstra’s Algorithm ก็จะทำให้ Time Complexity เป็น $\mathcal{O}(k + n \log n)$ (สมมุติว่า $n \approx m$)

Solution Code 3

บทสรุป

ตัวอย่าง 3 ข้อที่ยกมาอาจจะช่วยให้เห็นได้เพียงว่ามีเทคนิคแนวคิดแปลก ๆ ที่สามารถเอามาใช้กับการทำโจทย์ได้ แต่ก็อาจจะไม่ช่วยให้ทำโจทย์ได้มากขึ้นสักทีเดียว เพราะยังไง ๆ ก็ต้องใช้เวลาฝึกคิด/ฝึกโค้ดอยู่ดี ถ้าเป็นในไทยก็จะมีเว็บไซต์พวก programming.in.th, CodeCube, ProProg ที่มีโจทย์ดี ๆ เยอะแยะ ส่วนในต่างประเทศก็จะเป็นพวก Codeforces, TopCoder, CS Academy อะไรทำนองนี้

หวังว่าบทความนี้จะช่วยคนที่สนใจเรื่องอัลกอริทึม (โดยเฉพาะสาย Competitive Programmer) ได้ไม่มากก็น้อยครับ :)